Refine listing
Actions for selected content:
1095 results in 03xxx
Sur les collapses de corps différentiels colorés en caractéristique nulle décrits par Poizat à l'aide des amalgames à la Hrushovski
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 16 October 2008, pp. 445-464
- Print publication:
- July 2009
-
- Article
- Export citation
Groupes géométriques de rang de Morley fini
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 751-792
- Print publication:
- October 2008
-
- Article
- Export citation
Some questions concerning Hrushovski's amalgamation constructions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 793-823
- Print publication:
- October 2008
-
- Article
- Export citation
Expansions of fields by angular functions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 735-750
- Print publication:
- October 2008
-
- Article
- Export citation
La fusion libre : le cas simple
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 825-868
- Print publication:
- October 2008
-
- Article
- Export citation
GROUPS AND SEMIGROUPS WITH A ONE-COUNTER WORD PROBLEM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 197-209
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Difference fields and descent in algebraic dynamics. I
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 653-686
- Print publication:
- October 2008
-
- Article
- Export citation
Difference fields and descent in algebraic dynamics. II
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 687-704
- Print publication:
- October 2008
-
- Article
- Export citation
Genericity, generosity, and tori
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 705-722
- Print publication:
- October 2008
-
- Article
- Export citation
Circuits arithmétiques et calculs tensoriels
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 869-893
- Print publication:
- October 2008
-
- Article
- Export citation
Questions de corps de définition pour les variétés abéliennes en caractéristique positive
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 623-639
- Print publication:
- October 2008
-
- Article
- Export citation
On types of CB-rank 1 in simple theories
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 895-899
- Print publication:
- October 2008
-
- Article
- Export citation
De non ordinaria recognitione PSL2
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 723-734
- Print publication:
- October 2008
-
- Article
- Export citation
Linear Groups of Finite Morley Rank
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 04 April 2008, pp. 641-651
- Print publication:
- October 2008
-
- Article
- Export citation
Die böse Farbe
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 11 December 2007, pp. 415-443
- Print publication:
- July 2009
-
- Article
- Export citation
The block structure of complete lattice ordered effect algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 181-216
- Print publication:
- October 2007
-
- Article
-
- You have access
- Export citation
Perfect effect algebras are categorically equivalent with Abelian interpolation po-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-207
- Print publication:
- April 2007
-
- Article
-
- You have access
- Export citation
Filter games and pathological subgroups of a countable product of lines
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 321-350
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Free algebras in varieties of BL-algebras generated by a BLn-chain
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 419-439
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Loomis-Sikorski theorem for monotone σ-complete effect algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 305-318
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
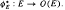 :
: 