The Archimedean components of triangular norms (which turn the closed unit interval into anabelian, totally ordered semigroup with neutral element 1) are studied, in particular their extension to triangular norms, and some construction methods for Archimedean components are given. The triangular norms which are uniquely determined by their Archimedean components are characterized. Using ordinal sums and additive generators, new types of left-continuous triangular norms are constructed.

Pseudoeffect (PE-) algebras generalize effect algebras by no longer being necessarily commutative. They are in certain cases representable as the unit interval of a unital po-group, for instance if they fulfil a certain Riesz property.

Several infinitary lattice properties and the countable Riesz interpolation property are studied for PE-algebras on the one hand and for po-groups on the other hand. We establish the exact relationships between the various conditions that are taken into account, and in particular, we examine how properties of a PE-algebra are related to the analogous properties of a representing po-group.

Modelling the distribution of mutations of mitochondrial DNA in exponentially growing cell cultures leads to the study of a multitype Galton–Watson process during its transient phase. The number of types corresponds to the number of mtDNA per cell and may be considered as large. By taking advantage of this fact we prove that the stochastic process is deterministic-like on the set of nonextinction. On this set almost all trajectories are well approximated by the unique solution of a partial differential problem. This result allows also the comparison of trajectories corresponding to different modelling assumptions, for instance different values of the number of types.

Pseudo-effect algebras are partial algebras (E; +, 0, 1) with a partially defined addition + which is not necessary commutative and with two complements, left and right ones. We define central elements of a pseudo-effect algebra and the centre, which in the case of MV-algebras coincides with the set of Boolean elements and in the case of effect algebras with the Riesz decomposition property central elements are only characteristic elements. If E satisfies general comparability, then E is a pseudo MV-algebra. Finally, we apply central elements to obtain a variation of the Cantor-Bernstein theorem for pseudo-effect algebras.

We show that any pseudo MV-algebra is isomorphic with an interval Γ(G, u), where G is an ℓ-group not necessarily Abelian with a strong unit u. In addition, we prove that the category of unital ℓ-groups is categorically equivalent with the category of pseudo MV-algebras. Since pseudo MV-algebras are a non-commutative generalization of MV-algebras, our assertions generalize a famous result of Mundici for a representation of MV-algebras by Abelian unital ℓ-groups. Our methods are completely different from those of Mundici. In addition, we show that any Archimedean pseudo MV-algebra is an MV-algebra.

In this paper, the variety of three-valued closure algebras, that is, closure algebras with the property that the open elements from a three-valued Heyting algebra, is investigated. Particularly, the structure of the finitely generated free objects in this variety is determined.

By blending techniques from set theory and algebraic topology we investigate the order of any homeomorphism of the nth power of the long ray or long line L having finite order, finding all possible orders when n = 1, 2, 3 or 4 in the first case and when n = 1 or 2 in the second. We also show that all finite powers of L are acyclic with respect to Alexander-Spanier cohomology.

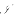Farah recently proved that many Borel P-ideals. on 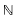satisfy the following requirement: any measurable homomorphism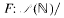 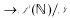has a continuous lifting 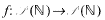which is a homomorphism itself. Ideals having such a property were called Radon–Nikodym (RN) ideals. Answering some Farah's questions, it is proved that many non-P ideals, including, for instance, Fin ⊗ Fin, are Radon–Nikodym. To prove this result, another property of ideals called the Fubini property, is introduced, which implies RN and is stable under some important transformations of ideals.

We show that every σ-complete MV-algebra is an MV-σ-homomorphic image of some σ-complete MV- algebra of fuzzy sets, called a tribe, which is a system of fuzzy sets of a crisp set Ω containing 1Ω and closed under fuzzy complementation and formation of min {∑nfn, 1}. Since a tribe is a direct generalization of a σ-algebra of crisp subsets, the representation theorem is an analogue of the Loomis-Sikorski theorem for MV-algebras. In addition, this result will be extended also for Dedekind σ-complete ℓ-groups with strong unit.

In this paper, given personnel distributions that are not attainable, we introduce the grade of attainability in order to measure the degree to which there exists a similar distribution that is attainable. For constant size systems controlled by recruitment, properties of the most similar distribution to a given distribution are formulated.

In this note we give an answer to the following problem of Todorcevic: Find out the combinatorial essence behind the fact that the family ℋ of the ground-model infinite sets of integers in a Perfect-set forcing extension has the property that for any Borel f: [ℕ]ω → {0, 1} there exists an A ∈ ℋ such that f is constant on [A]ω (see [7], [13]). In other words, one needs to capture the combinatorial properties of the family ℋ of ground-model subsets of ℕ which assure that it diagonalizes all Borel partitions. It turns out that the notion which results from our analysis of this problem is a bit more optimal than the older notion of a “happy family” (or selective coideal) introduced by A.R.D. Mathias [16] long ago in order to extend the well-known theorems of Galvin–Prikry [6] and Silver [25] (see Theorems 3.1 and 4.1 below). We should remark that these Mathias-style extensions can indeed be as useful in the applications as the original partition theorems.

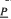A unified study is undertaken of finitely generated varieties HSP () of distributive lattices with unary operations, extending work of Cornish. The generating algebra () is assusmed to be of the form (P; ∧, ∨, 0, 1, {fμ}), where each fμ is an endomorphism or dual endomorphism of (P; ∧, ∨, 0, 1), and the Priestly dual of this lattice is an ordered semigroup N whose elements act by left multiplication to give the maps dual to the operations fμ. Duality theory is fully developed within this framework, into which fit many varieties arising in algebraic logic. Conditions on N are given for the natural and Priestley dualities for HSP () to be essentially the same, so that, inter alia, coproducts in HSP () are enriched D-coproducts.

It is known that every frame is isomorphic to the generalized Gleason algebra of an essentially unique bi-Stonian space (X, σ, τ) in which σ is T0. Let (X, σ, τ) be as above. The specialization order ≤σ, of (X, σ) is τ × τ-closed. By Nachbin's Theorem there is exactly one quasi-uniformity U on X such that ∩U = ≤σ and J(U*) = τ. This quasi-uniformity is compatible with σ and is coarser than the Pervin quasi-uniformity U of (X, σ). Consequently, τ is coarser than the Skula topology of σ and coincides with the Skula topology if and only if U = P.

Let C be a small category with weak finite limits, and let Flat(C) be the category of flat functors from C to the category of small sets. We prove that the free exact completion of C is the category of set-valued functors of Flat (C) which preserve small products and filtered colimits. In case C has finite limits, this gives A. Carboni and R. C. Magno's result on the free exact completion of a small category with finite limits.

In Zermelo-Fraenkel set theory weakened to permit the existence of atoms and without the axiom of choice we investigate the deductive strength of five statements which make assertions about the cardinality of the union of a well-ordered collection of sets. All five of the statements considered are consequences of the axiom of choice.

We prove that every locally finite, congruence modular, minimal variety is minimal as a quasivariety. We also construct all finite, strictly simple algebras generating a congruence distributive variety, such that the sett of unary term perations forms a group. Lastly, these results are applied to a problem in algebraic logic to give a sufficient condition for a deductive system to be structurally complete.

Countable homogeneous models are ‘simple’ objects from a model theoretic point of view. From a recursion theoretic point of view they can be complex. For instance the elementary theory of such a model might be undecidable, or the set of complete types might be recursively complex. Unfortunately even if neither of these conditions holds, such a model still can be undecidable. This paper investigates countable homogeneous models with respect to a weaker notion of decidability called almost decidable. It is shown that for theories that have only countably many type spectra, any countable homogeneous model of such a theory that has a Σ2 type spectrum is almost decidable.

We develop the idea of a θ-ordering (where θ is an infinite cardinal) for a family of infinite sets. A θ-ordering of the family A is a well ordering of A which decomposes A into a union of pairwise disjoint intervals in a special way, which facilitates certain transfinite constructions. We show that several standard combinatorial properties, for instance that of the family A having a θ-transversal, are simple consequences of A possessing a θ-ordering. Most of the paper is devoted to showing that under suitable restrictions, an almost disjoint family will have a θ-ordering. The restrictions involve either intersection conditions on A (the intersection of every λ-size subfamily of A has size at most κ) or a chain condition on A.

Recursively presented topological spaces are topological spaces with a recursive system of basic neighbourhoods. A recursively enumerable (r.e.) open set is a r.e. union of basic neighbourhoods. A set is everywhere r.e. open if its intersection with each basic neighbourhood is r.e. Similarly we define everywhere creative, everywhere simple, everywhere r.e. non-recursive sets and show that there exist sets both with and without these everywhere properties.

Notions of effective complementation in effective topological spaces are considered, and several types of non-complemented sets are constructed. While there are parallels with recursively enumerable sets, some unexpected differences appear. Finally, a pair of splitting theorems is proved.