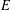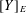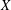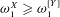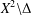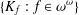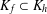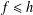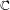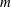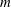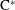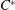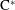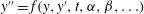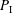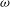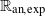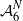Refine listing
Actions for selected content:
1095 results in 03xxx
SOME PROPERTIES OF ANALYTIC DIFFERENCE VALUED FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 29 May 2015, pp. 447-499
- Print publication:
- June 2017
-
- Article
- Export citation
ANALYTIC EQUIVALENCE RELATIONS SATISFYING HYPERARITHMETIC-IS-RECURSIVE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 27 April 2015, e8
-
- Article
-
- You have access
- Open access
- Export citation
First-Order Convergence and Roots†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 24 February 2015, pp. 213-221
-
- Article
- Export citation
DOMINATION CONDITIONS UNDER WHICH A COMPACT SPACE IS METRISABLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 11 February 2015, pp. 502-507
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
LOCAL INTERDEFINABILITY OF WEIERSTRASS ELLIPTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 24 November 2014, pp. 673-691
- Print publication:
- October 2016
-
- Article
- Export citation
Equivalences in Euler-based diagram systems through normal forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 431-484
-
- Article
-
- You have access
- Export citation
Computing boundary extensions of conformal maps
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 360-378
-
- Article
-
- You have access
- Export citation
COMPARING
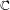 $\mathbb{C}$ AND ZILBER’S EXPONENTIAL FIELDS: ZERO SETS OF EXPONENTIAL POLYNOMIALS
$\mathbb{C}$ AND ZILBER’S EXPONENTIAL FIELDS: ZERO SETS OF EXPONENTIAL POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 04 August 2014, pp. 71-84
- Print publication:
- January 2016
-
- Article
- Export citation
THE REFLEXIVITY INDEX OF A LATTICE OF SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 237-250
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
RIGIDITY OF CONTINUOUS QUOTIENTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2014, pp. 1-28
- Print publication:
- January 2016
-
- Article
- Export citation
ASPECTS OF GLOBULAR HIGHER CATEGORY THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 19 May 2014, pp. 172-173
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
FREE GROUPS AND AUTOMORPHISM GROUPS OF INFINITE STRUCTURES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 17 April 2014, e8
-
- Article
-
- You have access
- Open access
- Export citation
Deterministic polynomial factoring and association schemes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 123-140
-
- Article
-
- You have access
- Export citation
A NONSEPARABLE AMENABLE OPERATOR ALGEBRA WHICH IS NOT ISOMORPHIC TO A
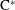 $C^*$ -ALGEBRA
$C^*$ -ALGEBRA
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 March 2014, e2
-
- Article
-
- You have access
- Open access
- Export citation
On the algebraic independence of generic Painlevé transcendents
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 668-678
- Print publication:
- April 2014
-
- Article
- Export citation
Cartan subgroups of groups definable ino-minimal structures
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 28 November 2013, pp. 849-893
- Print publication:
- October 2014
-
- Article
- Export citation
Applications du théorème d’Ax–Lindemann hyperbolique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 2 / February 2014
- Published online by Cambridge University Press:
- 19 November 2013, pp. 175-190
- Print publication:
- February 2014
-
- Article
- Export citation
SPECIAL POINT PROBLEMS WITH ELLIPTIC MODULAR SURFACES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 06 November 2013, pp. 1-31
- Print publication:
- January 2014
-
- Article
- Export citation
Stationary reflection principles and two cardinal tree properties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 01 November 2013, pp. 69-85
- Print publication:
- January 2015
-
- Article
- Export citation
SUPERNILPOTENCE PREVENTS DUALIZABILITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 30 September 2013, pp. 1-24
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation