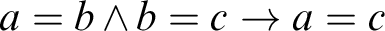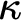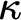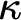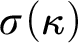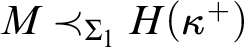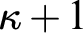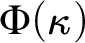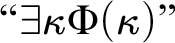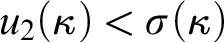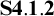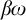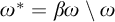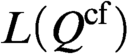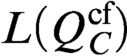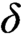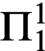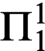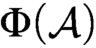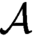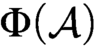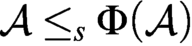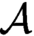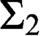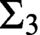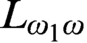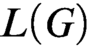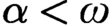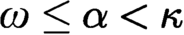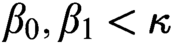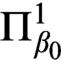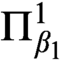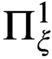Refine listing
Actions for selected content:
1095 results in 03xxx
WITTGENSTEIN’S ELIMINATION OF IDENTITY FOR QUANTIFIER-FREE LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 June 2020, pp. 1-21
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MITCHELL-INSPIRED FORCING, WITH SMALL WORKING PARTS AND COLLECTIONS OF MODELS OF UNIFORM SIZE AS SIDE CONDITIONS, AND GAP-ONE SIMPLIFIED MORASSES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 22 June 2020, pp. 392-415
- Print publication:
- March 2022
-
- Article
- Export citation
THE LOGIC OF COMPARATIVE CARDINALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 22 June 2020, pp. 972-1005
- Print publication:
- September 2020
-
- Article
- Export citation
STABLY MEASURABLE CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 15 June 2020, pp. 448-470
- Print publication:
- June 2021
-
- Article
- Export citation
COMPLETELY SEPARABLE MAD FAMILIES AND THE MODAL LOGIC OF βω
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 15 June 2020, pp. 498-507
- Print publication:
- June 2022
-
- Article
- Export citation
AN EXPOSITION OF THE COMPACTNESS OF
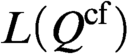 $L({Q^{\mathrm{cf}}})$
$L({Q^{\mathrm{cf}}})$
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 11 June 2020, pp. 212-218
- Print publication:
- December 2020
-
- Article
- Export citation
GÖDEL’S SECOND INCOMPLETENESS THEOREM: HOW IT IS DERIVED AND WHAT IT DELIVERS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 10 June 2020, pp. 241-256
- Print publication:
- December 2020
-
- Article
- Export citation
INTERPRETABILITY LOGICS AND GENERALISED VELTMAN SEMANTICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 749-772
- Print publication:
- June 2020
-
- Article
- Export citation
N-BERKELEY CARDINALS AND WEAK EXTENDER MODELS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 809-816
- Print publication:
- June 2020
-
- Article
- Export citation
HOMOGENEOUS STRUCTURES WITH NONUNIVERSAL AUTOMORPHISM GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 22 June 2020, pp. 817-827
- Print publication:
- June 2020
-
- Article
- Export citation
THE KETONEN ORDER
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 585-604
- Print publication:
- June 2020
-
- Article
- Export citation
EXACT COMPLETION AND CONSTRUCTIVE THEORIES OF SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 563-584
- Print publication:
- June 2020
-
- Article
-
- You have access
- Open access
- Export citation
FIRST-ORDER RECOGNIZABILITY IN FINITE AND PSEUDOFINITE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 852-867
- Print publication:
- June 2020
-
- Article
- Export citation
HOW STRONG ARE SINGLE FIXED POINTS OF NORMAL FUNCTIONS?
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 709-732
- Print publication:
- June 2020
-
- Article
- Export citation
EQUATIONAL THEORIES OF FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 828-851
- Print publication:
- June 2020
-
- Article
- Export citation
THE COMPLEXITY OF HOMEOMORPHISM RELATIONS ON SOME CLASSES OF COMPACTA
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 733-748
- Print publication:
- June 2020
-
- Article
- Export citation
CODING IN GRAPHS AND LINEAR ORDERINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 673-690
- Print publication:
- June 2020
-
- Article
- Export citation
A REFINEMENT OF THE RAMSEY HIERARCHY VIA INDESCRIBABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 22 June 2020, pp. 773-808
- Print publication:
- June 2020
-
- Article
- Export citation
ON CONFIGURATIONS CONCERNING CARDINAL CHARACTERISTICS AT REGULAR CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 10 July 2020, pp. 691-708
- Print publication:
- June 2020
-
- Article
- Export citation
A RECONSTRUCTION OF STEEL’S MULTIVERSE PROJECT
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 11 June 2020, pp. 118-169
- Print publication:
- June 2020
-
- Article
-
- You have access
- Open access
- Export citation