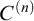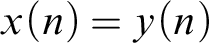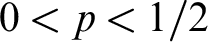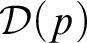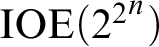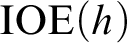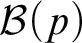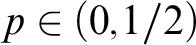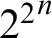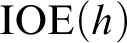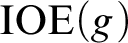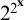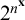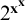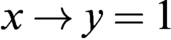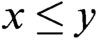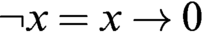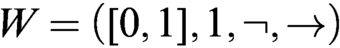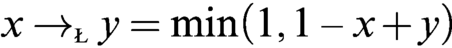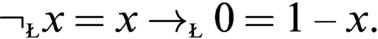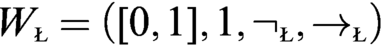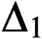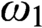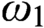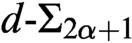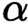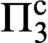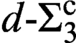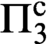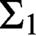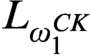Refine listing
Actions for selected content:
1095 results in 03xxx
THE TREE OF TUPLES OF A STRUCTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 07 September 2020, pp. 21-46
- Print publication:
- March 2022
-
- Article
- Export citation
MULTIDIMENSIONAL EXACT CLASSES, SMOOTH APPROXIMATION AND BOUNDED 4-TYPES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1305-1341
- Print publication:
- December 2020
-
- Article
- Export citation
IDENTITY CRISIS BETWEEN SUPERCOMPACTNESS AND VǑPENKA’S PRINCIPLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 07 September 2020, pp. 626-648
- Print publication:
- June 2022
-
- Article
- Export citation
MUCHNIK DEGREES AND CARDINAL CHARACTERISTICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 04 September 2020, pp. 471-498
- Print publication:
- June 2021
-
- Article
- Export citation
ASYMPTOTIC ANALYSIS OF SKOLEM’S EXPONENTIAL FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 04 September 2020, pp. 758-782
- Print publication:
- June 2022
-
- Article
- Export citation
INFINITARY GENERALIZATIONS OF DELIGNE’S COMPLETENESS THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 1147-1162
- Print publication:
- September 2020
-
- Article
- Export citation
ON THE COMPLEXITY OF CLASSIFYING LEBESGUE SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 26 October 2020, pp. 1254-1288
- Print publication:
- September 2020
-
- Article
- Export citation
GÖDEL DIFFEOMORPHISMS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 01 September 2020, pp. 219-223
- Print publication:
- December 2020
-
- Article
- Export citation
WHAT THE ŁUKASIEWICZ AXIOMS MEAN
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 30 October 2020, pp. 906-917
- Print publication:
- September 2020
-
- Article
- Export citation
CATEGORICAL SEMANTICS OF METRIC SPACES AND CONTINUOUS LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1044-1078
- Print publication:
- September 2020
-
- Article
- Export citation
PROVABLY
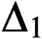 $\Delta_1$ GAMES
$\Delta_1$ GAMES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 30 October 2020, pp. 1124-1146
- Print publication:
- September 2020
-
- Article
- Export citation
DECOMPOSING FUNCTIONS OF BAIRE CLASS
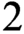 $2$ ON POLISH SPACES
$2$ ON POLISH SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 26 October 2020, pp. 960-971
- Print publication:
- September 2020
-
- Article
- Export citation
THE COMPLEXITY OF SCOTT SENTENCES OF SCATTERED LINEAR ORDERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 23 October 2020, pp. 1079-1101
- Print publication:
- September 2020
-
- Article
- Export citation
A NOTE ON DERIVABILITY CONDITIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1224-1253
- Print publication:
- September 2020
-
- Article
- Export citation
STATIONARY REFLECTION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 08 January 2021, pp. 937-959
- Print publication:
- September 2020
-
- Article
- Export citation
BASES FOR FUNCTIONS BEYOND THE FIRST BAIRE CLASS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1289-1303
- Print publication:
- September 2020
-
- Article
- Export citation
A SIMPLIFIED ORDINAL ANALYSIS OF FIRST-ORDER REFLECTION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 23 October 2020, pp. 1163-1185
- Print publication:
- September 2020
-
- Article
- Export citation
ON A GENERALIZED FRAÏSSÉ LIMIT CONSTRUCTION AND ITS APPLICATION TO THE JIANG–SU ALGEBRA
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 23 October 2020, pp. 1186-1223
- Print publication:
- September 2020
-
- Article
- Export citation
DIMENSIONAL GROUPS AND FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 918-936
- Print publication:
- September 2020
-
- Article
- Export citation
THE POTENTIAL IN FREGE’S THEOREM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 August 2020, pp. 553-577
- Print publication:
- June 2023
-
- Article
- Export citation