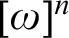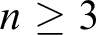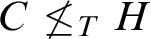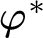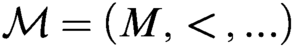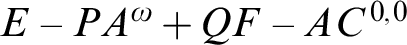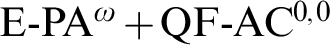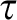Refine listing
Actions for selected content:
1095 results in 03xxx
INQUISITIVE BISIMULATION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 77-109
- Print publication:
- March 2021
-
- Article
- Export citation
THE KIM–PILLAY THEOREM FOR ABSTRACT ELEMENTARY CATEGORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 October 2020, pp. 1717-1741
- Print publication:
- December 2020
-
- Article
- Export citation
WEIHRAUCH GOES BROUWERIAN
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 October 2020, pp. 1614-1653
- Print publication:
- December 2020
-
- Article
- Export citation
LUZIN’S (N) AND RANDOMNESS REFLECTION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 30 October 2020, pp. 802-828
- Print publication:
- June 2022
-
- Article
- Export citation
RAMSEY-LIKE THEOREMS AND MODULI OF COMPUTATION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 27 October 2020, pp. 72-108
- Print publication:
- March 2022
-
- Article
- Export citation
THE MODAL LOGICS OF KRIPKE–FEFERMAN TRUTH
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 27 October 2020, pp. 362-396
- Print publication:
- March 2021
-
- Article
- Export citation
AROUND RUBIN’S “THEORIES OF LINEAR ORDER”
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1403-1426
- Print publication:
- December 2020
-
- Article
- Export citation
Cardinal invariants of Haar null and Haar meager sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1568-1594
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
THE CHARACTERIZATION OF WEIHRAUCH REDUCIBILITY IN SYSTEMS CONTAINING
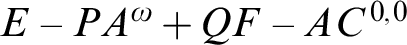 $E-PA^{\omega } + QF-AC^{0,0}$
$E-PA^{\omega } + QF-AC^{0,0}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 27 October 2020, pp. 224-261
- Print publication:
- March 2021
-
- Article
- Export citation
PSEUDO-FINITE SETS, PSEUDO-O-MINIMALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 26 October 2020, pp. 577-599
- Print publication:
- June 2021
-
- Article
- Export citation
ELEMENTARY EQUIVALENCE THEOREM FOR PAC STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 26 October 2020, pp. 1467-1498
- Print publication:
- December 2020
-
- Article
- Export citation
COMPUTABILITY OF POLISH SPACES UP TO HOMEOMORPHISM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 26 October 2020, pp. 1664-1686
- Print publication:
- December 2020
-
- Article
- Export citation
COMPUTABILITY, ORDERS, AND SOLVABLE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 22 October 2020, pp. 1588-1598
- Print publication:
- December 2020
-
- Article
- Export citation
A PREDICATIVE VARIANT OF HYLAND’S EFFECTIVE TOPOS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 22 October 2020, pp. 433-447
- Print publication:
- June 2021
-
- Article
- Export citation
PUNCTUAL CATEGORICITY AND UNIVERSALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 22 October 2020, pp. 1427-1466
- Print publication:
- December 2020
-
- Article
- Export citation
STRONGLY MINIMAL STEINER SYSTEMS I: EXISTENCE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 October 2020, pp. 1486-1507
- Print publication:
- December 2021
-
- Article
- Export citation
DOING WITHOUT ACTION TYPES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 380-410
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXPLORING THE LANDSCAPE OF RELATIONAL SYLLOGISTIC LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 728-765
- Print publication:
- September 2021
-
- Article
- Export citation
SEMANTICS FOR PURE THEORIES OF CONNEXIVE IMPLICATION
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 October 2020, pp. 591-606
- Print publication:
- September 2022
-
- Article
- Export citation
KOLMOGOROV CONDITIONALIZERS CAN BE DUTCH BOOKED (IF AND ONLY IF THEY ARE EVIDENTIALLY UNCERTAIN)
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 October 2020, pp. 722-757
- Print publication:
- September 2022
-
- Article
- Export citation