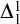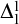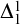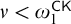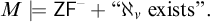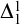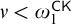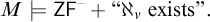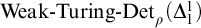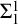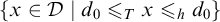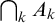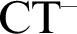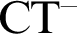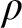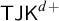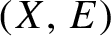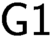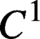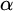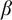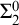Refine listing
Actions for selected content:
1095 results in 03xxx
VARIATIONS ON
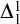 $\Delta ^{1}_{1}$ DETERMINACY AND ℵω1
$\Delta ^{1}_{1}$ DETERMINACY AND ℵω1
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 07 January 2021, pp. 721-731
- Print publication:
- June 2022
-
- Article
- Export citation
DISJUNCTIONS WITH STOPPING CONDITIONS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 05 January 2021, pp. 231-253
- Print publication:
- September 2021
-
- Article
- Export citation
CURRENT RESEARCH ON GÖDEL’S INCOMPLETENESS THEOREMS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 05 January 2021, pp. 113-167
- Print publication:
- June 2021
-
- Article
- Export citation
On Polish groups admitting non-essentially countable actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 180-194
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Proof of a conjecture of Galvin
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 21 December 2020, e15
-
- Article
-
- You have access
- Open access
- Export citation
WHAT IS A RULE OF INFERENCE?
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 21 December 2020, pp. 307-346
- Print publication:
- June 2021
-
- Article
- Export citation
BINARY KRIPKE SEMANTICS FOR A STRONG LOGIC FOR NAIVE TRUTH
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 December 2020, pp. 668-692
- Print publication:
- September 2022
-
- Article
- Export citation
A characterization of singular Schrödinger operators on the half-line
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 07 December 2020, pp. 923-941
- Print publication:
- December 2021
-
- Article
- Export citation
Decompositions and measures on countable Borel equivalence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 04 December 2020, pp. 3671-3703
- Print publication:
- December 2021
-
- Article
- Export citation
THE MODAL LOGIC OF
 $\sigma $-CENTERED FORCING AND RELATED FORCING CLASSES
$\sigma $-CENTERED FORCING AND RELATED FORCING CLASSES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1-24
- Print publication:
- March 2021
-
- Article
- Export citation
TWO ARGUMENTS AGAINST THE GENERIC MULTIVERSE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 02 December 2020, pp. 347-379
- Print publication:
- June 2021
-
- Article
- Export citation
BOUNDS FOR INDEXES OF NILPOTENCY IN COMMUTATIVE RING THEORY: A PROOF MINING APPROACH
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 05 January 2021, pp. 257-267
- Print publication:
- December 2020
-
- Article
- Export citation
LIFSCHITZ REALIZABILITY AS A TOPOLOGICAL CONSTRUCTION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1342-1375
- Print publication:
- December 2020
-
- Article
- Export citation
FINDING THE LIMIT OF INCOMPLETENESS I
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 16 April 2021, pp. 268-286
- Print publication:
- December 2020
-
- Article
- Export citation
COMPUTABILITY IN PARTIAL COMBINATORY ALGEBRAS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 05 January 2021, pp. 224-240
- Print publication:
- December 2020
-
- Article
-
- You have access
- Open access
- Export citation
The Brouwer invariance theorems in reverse mathematics
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e51
-
- Article
-
- You have access
- Open access
- Export citation
RANK-TO-RANK EMBEDDINGS AND STEEL’S CONJECTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 137-147
- Print publication:
- March 2021
-
- Article
- Export citation
A dichotomy of sets via typical differentiability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 04 November 2020, e41
-
- Article
-
- You have access
- Open access
- Export citation
CUPPING AND JUMP CLASSES IN THE COMPUTABLY ENUMERABLE DEGREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 October 2020, pp. 1499-1545
- Print publication:
- December 2020
-
- Article
- Export citation
INFINITE STRINGS AND THEIR LARGE SCALE PROPERTIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 30 October 2020, pp. 585-625
- Print publication:
- June 2022
-
- Article
- Export citation