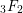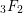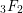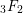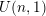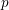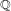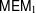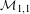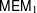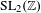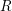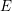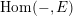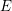Refine listing
Actions for selected content:
539 results in 11Gxx
COMPACTIFICATIONS OF SUBSCHEMES OF INTEGRAL MODELS OF SHIMURA VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 24 September 2018, e18
-
- Article
-
- You have access
- Open access
- Export citation
A FUNCTIONAL LOGARITHMIC FORMULA FOR THE HYPERGEOMETRIC FUNCTION
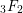 $_{3}F_{2}$
$_{3}F_{2}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 14 September 2018, pp. 29-46
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
AN ALGEBRO-GEOMETRIC STUDY OF SPECIAL VALUES OF HYPERGEOMETRIC FUNCTIONS
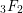 $_{3}F_{2}$
$_{3}F_{2}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 13 September 2018, pp. 47-62
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
On two arithmetic theta lifts
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 07 September 2018, pp. 2090-2149
- Print publication:
- October 2018
-
- Article
- Export citation
RAPOPORT–ZINK UNIFORMIZATION OF HODGE-TYPE SHIMURA VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 03 September 2018, e16
-
- Article
-
- You have access
- Open access
- Export citation
Constructing elliptic curves from Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 29 August 2018, pp. 2045-2054
- Print publication:
- October 2018
-
- Article
- Export citation
Applications of the hyperbolic Ax–Schanuel conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 13 August 2018, pp. 1843-1888
- Print publication:
- September 2018
-
- Article
- Export citation
The Manin constant in the semistable case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 13 August 2018, pp. 1889-1920
- Print publication:
- September 2018
-
- Article
- Export citation
SINGULARITIES OF THE BIEXTENSION METRIC FOR FAMILIES OF ABELIAN VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 23 July 2018, e12
-
- Article
-
- You have access
- Open access
- Export citation
COMPARING THE BRAUER GROUP TO THE TATE–SHAFAREVICH GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 19 July 2018, pp. 965-970
- Print publication:
- May 2020
-
- Article
- Export citation
Finiteness theorems for K3 surfaces and abelian varieties of CM type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 1571-1592
- Print publication:
- August 2018
-
- Article
- Export citation
A SIMPLE PROOF OF CHEBOTAREV’S DENSITY THEOREM OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 12 July 2018, pp. 196-202
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Siegel families with application to class fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 27 June 2018, pp. 751-771
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Arithmetical Power Series Expansion of the Sigma Function for a Plane Curve
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 995-1022
-
- Article
- Export citation
DISTINGUISHED MODELS OF INTERMEDIATE JACOBIANS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 08 June 2018, pp. 891-918
- Print publication:
- May 2020
-
- Article
- Export citation
INTEGRAL AND ADELIC ASPECTS OF THE MUMFORD–TATE CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 07 June 2018, pp. 869-890
- Print publication:
- May 2020
-
- Article
- Export citation
Arithmetic intersection on GSpin Rapoport–Zink spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1407-1440
- Print publication:
- July 2018
-
- Article
- Export citation
UNIVERSAL MIXED ELLIPTIC MOTIVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 30 April 2018, pp. 663-766
- Print publication:
- May 2020
-
- Article
- Export citation
A VARIATION ON THE THEME OF NICOMACHUS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 367-373
- Print publication:
- June 2018
-
- Article
-
- You have access
- Open access
- Export citation
Abelian varieties isogenous to a power of an elliptic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 21 March 2018, pp. 934-959
- Print publication:
- May 2018
-
- Article
- Export citation