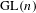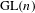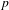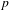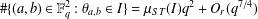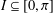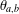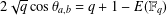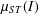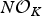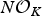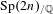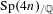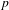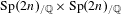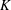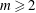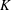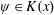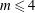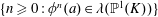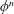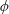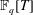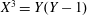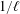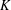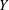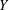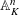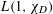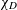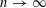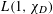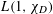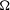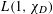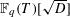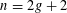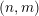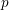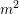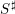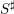Refine listing
Actions for selected content:
539 results in 11Gxx
PARITY OF THE LANGLANDS PARAMETERS OF CONJUGATE SELF-DUAL REPRESENTATIONS OF
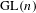 $\text{GL}(n)$ AND THE LOCAL JACQUET–LANGLANDS CORRESPONDENCE
$\text{GL}(n)$ AND THE LOCAL JACQUET–LANGLANDS CORRESPONDENCE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 19 February 2019, pp. 2017-2043
- Print publication:
- November 2020
-
- Article
- Export citation
ON THE
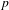 $p$-ADIC VARIATION OF HEEGNER POINTS
$p$-ADIC VARIATION OF HEEGNER POINTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 18 February 2019, pp. 2127-2164
- Print publication:
- November 2020
-
- Article
- Export citation
On the Schertz Conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 08 February 2019, pp. 837-845
-
- Article
- Export citation
THE ERROR TERM IN THE SATO–TATE THEOREM OF BIRCH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 08 February 2019, pp. 27-33
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Binary quadratic forms and ray class groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 695-720
- Print publication:
- April 2020
-
- Article
- Export citation
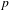 $p$-ADIC
$p$-ADIC  $L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS
$L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 14 January 2019, pp. 1287-1347
- Print publication:
- July 2020
-
- Article
- Export citation
Powers in Orbits of Rational Functions: Cases of an Arithmetic Dynamical Mordell–Lang Conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 773-817
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Cubic Twin Prime Polynomials are Counted by a Modular Form
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1323-1350
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Logarithmes des points rationnels des variétés abéliennes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 247-298
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Sharp Bertini Theorem for Plane Curves over Finite Fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 223-230
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
The Hermite–Joubert Problem and a Conjecture of Brassil and Reichstein
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 169-177
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
ON THE DISTRIBUTION OF THE RATIONAL POINTS ON CYCLIC COVERS IN THE ABSENCE OF ROOTS OF UNITY
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 17 April 2019, pp. 719-742
- Print publication:
- 2019
-
- Article
- Export citation
MODELS OF TORSORS OVER AFFINE SPACES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 530-541
- Print publication:
- 2019
-
- Article
- Export citation
Mean values of derivatives of L-functions in function fields: III
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 905-913
- Print publication:
- August 2019
-
- Article
- Export citation
HASSE PRINCIPLES FOR ÉTALE MOTIVIC COHOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 63-83
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
DUALITY FOR COHOMOLOGY OF CURVES WITH COEFFICIENTS IN ABELIAN VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 42-149
- Print publication:
- December 2020
-
- Article
- Export citation
COMPLEX MOMENTS AND THE DISTRIBUTION OF VALUES OF
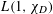 $L(1,\unicode[STIX]{x1D712}_{D})$ OVER FUNCTION FIELDS WITH APPLICATIONS TO CLASS NUMBERS
$L(1,\unicode[STIX]{x1D712}_{D})$ OVER FUNCTION FIELDS WITH APPLICATIONS TO CLASS NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 05 December 2018, pp. 236-271
- Print publication:
- 2019
-
- Article
- Export citation
A Modular André–Oort Statement with Derivatives
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 323-365
-
- Article
- Export citation
Foliations on unitary Shimura varieties in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 11 October 2018, pp. 2267-2304
- Print publication:
- November 2018
-
- Article
- Export citation
HIGHER IDELES AND CLASS FIELD THEORY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 02 October 2018, pp. 214-250
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation