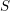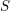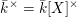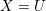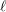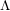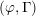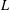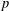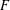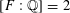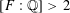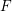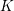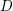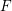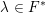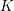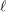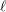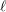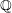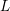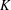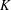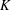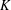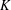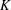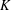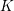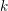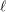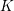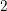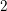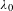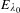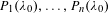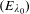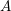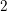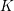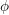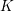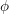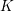Refine listing
Actions for selected content:
539 results in 11Gxx
PERIODS OF DRINFELD MODULES AND LOCAL SHTUKAS WITH COMPLEX MULTIPLICATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 20 March 2018, pp. 175-208
- Print publication:
- January 2020
-
- Article
- Export citation
Approximation forte pour les variétés avec une action d’un groupe linéaire
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 773-819
- Print publication:
- April 2018
-
- Article
- Export citation
Cycles in the de Rham cohomology of abelian varieties over number fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 850-882
- Print publication:
- April 2018
-
- Article
- Export citation
The geometry of Hida families II:
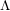 $\unicode[STIX]{x1D6EC}$ -adic
$\unicode[STIX]{x1D6EC}$ -adic 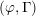 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules and
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules and 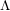 $\unicode[STIX]{x1D6EC}$ -adic Hodge theory
$\unicode[STIX]{x1D6EC}$ -adic Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 719-760
- Print publication:
- April 2018
-
- Article
- Export citation
ALGEBRAIC TORI AS DEGENERATIONS OF ABELIAN VARIETIES
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 303-329
- Print publication:
- 2018
-
- Article
-
- You have access
- HTML
- Export citation
TRUNCATED PRODUCT REPRESENTATIONS FOR
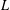 $L$ -FUNCTIONS IN THE HYPERELLIPTIC ENSEMBLE
$L$ -FUNCTIONS IN THE HYPERELLIPTIC ENSEMBLE
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 06 February 2018, pp. 137-158
- Print publication:
- 2018
-
- Article
- Export citation
Corrigendum: Torsion points on abelian varieties of CM-type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 26 December 2017, p. 594
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
UNRAMIFIEDNESS OF GALOIS REPRESENTATIONS ARISING FROM HILBERT MODULAR SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 23 November 2017, e29
-
- Article
-
- You have access
- Open access
- Export citation
Local–global principle for reduced norms over function fields of
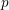 $p$ -adic curves
$p$ -adic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 410-458
- Print publication:
- February 2018
-
- Article
- Export citation
ON THE RESIDUE OF EISENSTEIN CLASSES OF SIEGEL VARIETIES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 539-553
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
A MODULI INTERPRETATION FOR THE NON-SPLIT CARTAN MODULAR CURVE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 411-434
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
LOCAL BORCHERDS PRODUCTS FOR UNITARY GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 27 October 2017, pp. 139-169
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
Around
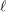 $\ell$ -independence
$\ell$ -independence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 223-248
- Print publication:
- January 2018
-
- Article
- Export citation
Rational points on hyperelliptic curves having a marked non-Weierstrass point
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 188-222
- Print publication:
- January 2018
-
- Article
- Export citation
Nearby cycles of automorphic étale sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 05 October 2017, pp. 80-119
- Print publication:
- January 2018
-
- Article
- Export citation
ON PERFECT
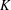 $K$ -RATIONAL CUBOIDS
$K$ -RATIONAL CUBOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 26-32
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Good reduction of K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 18 September 2017, pp. 1-35
- Print publication:
- January 2018
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bad reduction of genus
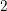 $2$ curves with CM jacobian varieties
$2$ curves with CM jacobian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 11 September 2017, pp. 2534-2576
- Print publication:
- December 2017
-
- Article
- Export citation
CM RELATIONS IN FIBERED POWERS OF ELLIPTIC FAMILIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 02 August 2017, pp. 941-956
- Print publication:
- September 2019
-
- Article
- Export citation
EXPLICIT SURJECTIVITY RESULTS FOR DRINFELD MODULES OF RANK 2
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 27 July 2017, pp. 17-45
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation