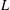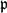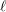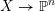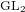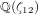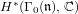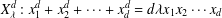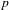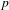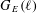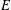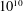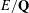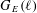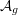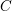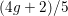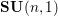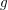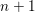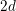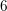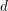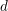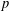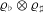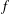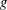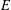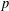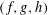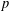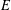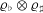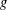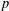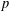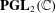Refine listing
Actions for selected content:
539 results in 11Gxx
ANDRÉ–OORT CONJECTURE AND NONVANISHING OF CENTRAL
 $L$ -VALUES OVER HILBERT CLASS FIELDS
$L$ -VALUES OVER HILBERT CLASS FIELDS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 20 July 2016, e20
-
- Article
-
- You have access
- Open access
- Export citation
COMPUTING L-FUNCTIONS AND SEMISTABLE REDUCTION OF SUPERELLIPTIC CURVES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 77-108
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
Level raising mod 2 and arbitrary 2-Selmer ranks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 1576-1608
- Print publication:
- August 2016
-
- Article
- Export citation
On some Fricke families and application to the Lang–Schertz conjecture
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 18 May 2016, pp. 723-740
- Print publication:
- August 2016
-
- Article
- Export citation
TWISTED GALOIS STRATIFICATION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 222 / Issue 1 / June 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 1-60
- Print publication:
- June 2016
-
- Article
-
- You have access
- HTML
- Export citation
Failures of weak approximation in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 26 April 2016, pp. 1435-1475
- Print publication:
- July 2016
-
- Article
- Export citation
Modular elliptic curves over the field of twelfth roots of unity
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 155-174
-
- Article
-
- You have access
- Export citation
GENERALIZED EXPLICIT DESCENT AND ITS APPLICATION TO CURVES OF GENUS 3
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, e6
-
- Article
-
- You have access
- Open access
- Export citation
COUNTING POINTS ON DWORK HYPERSURFACES AND
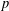 $p$ -ADIC HYPERGEOMETRIC FUNCTIONS
$p$ -ADIC HYPERGEOMETRIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 208-216
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
ON THE EXCEPTIONAL SPECIALIZATIONS OF BIG HEEGNER POINTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 February 2016, pp. 207-240
- Print publication:
- February 2018
-
- Article
- Export citation
COMPUTING IMAGES OF GALOIS REPRESENTATIONS ATTACHED TO ELLIPTIC CURVES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 02 February 2016, e4
-
- Article
-
- You have access
- Open access
- Export citation
On the Oort conjecture for Shimura varieties of unitary and orthogonal types
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 889-917
- Print publication:
- May 2016
-
- Article
- Export citation
COMPACTIFICATIONS OF PEL-TYPE SHIMURA VARIETIES IN RAMIFIED CHARACTERISTICS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 05 January 2016, e1
-
- Article
-
- You have access
- Open access
- Export citation
THE PROPORTION OF FAILURES OF THE HASSE NORM PRINCIPLE
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 337-347
- Print publication:
- 2016
-
- Article
- Export citation
Strict supports of canonical measures and applications to the geometric Bogomolov conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 997-1040
- Print publication:
- May 2016
-
- Article
- Export citation
Integral canonical models for Spin Shimura varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 07 December 2015, pp. 769-824
- Print publication:
- April 2016
-
- Article
- Export citation
Good families of Drinfeld modular curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 699-712
-
- Article
-
- You have access
- Export citation
Integral points of bounded degree on affine curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 26 November 2015, pp. 754-768
- Print publication:
- April 2016
-
- Article
- Export citation
CERTAIN GENERALIZED MORDELL CURVES OVER THE RATIONAL NUMBERS ARE POINTLESS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 28 October 2015, pp. 42-64
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
STARK POINTS AND
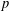 $p$-ADIC ITERATED INTEGRALS ATTACHED TO MODULAR FORMS OF WEIGHT ONE
$p$-ADIC ITERATED INTEGRALS ATTACHED TO MODULAR FORMS OF WEIGHT ONE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 13 October 2015, e8
-
- Article
-
- You have access
- Open access
- Export citation