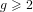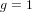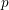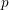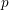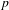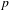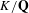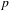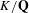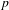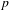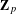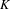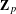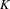Refine listing
Actions for selected content:
539 results in 11Gxx
Simply connected varieties in characteristic
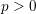 $p>0$
$p>0$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 09 October 2015, pp. 255-287
- Print publication:
- February 2016
-
- Article
- Export citation
CATEGORICITY OF MODULAR AND SHIMURA CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 30 September 2015, pp. 1075-1101
- Print publication:
- November 2017
-
- Article
- Export citation
The Chowla–Selberg formula for abelian CM fields and Faltings heights
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 24 September 2015, pp. 445-476
- Print publication:
- March 2016
-
- Article
- Export citation
Mordell’s equation: a classical approach
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 September 2015, pp. 633-646
-
- Article
-
- You have access
- Export citation
p-adic Eisenstein-Kronecker series for CM elliptic curves and the Kronecker limit formulas
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 269-302
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
PARAMETRIZING ELLIPTIC CURVES BY MODULAR UNITS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 19 August 2015, pp. 33-41
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
NON-ARCHIMEDEAN YOMDIN–GROMOV PARAMETRIZATIONS AND POINTS OF BOUNDED HEIGHT
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 14 August 2015, e5
-
- Article
-
- You have access
- Open access
- Export citation
Formal Fourier Jacobi expansions and special cycles of codimension two
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 06 August 2015, pp. 2187-2211
- Print publication:
- December 2015
-
- Article
- Export citation
Examples of CM curves of genus two defined over the reflex field
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 August 2015, pp. 507-538
-
- Article
-
- You have access
- Export citation
Hyperelliptic modular curves
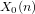 $X_{0}(n)$ and isogenies of elliptic curves over quadratic fields
$X_{0}(n)$ and isogenies of elliptic curves over quadratic fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 August 2015, pp. 578-602
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF RATIONAL POINTS ON PRYM VARIETIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 55-68
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
EXCEPTIONAL ZEROES OF P-ADIC L-FUNCTIONS OVER NON-ABELIAN FIELD EXTENSIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 385-432
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
Growth of
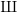 $\unicode[STIX]{x0428}$ in towers for isogenous curves
$\unicode[STIX]{x0428}$ in towers for isogenous curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 30 June 2015, pp. 1981-2005
- Print publication:
- November 2015
-
- Article
- Export citation
Le complémentaire des puissances
 $n$-ièmes dans un corps de nombres est un ensemble diophantien
$n$-ièmes dans un corps de nombres est un ensemble diophantien
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 10 / October 2015
- Published online by Cambridge University Press:
- 22 June 2015, pp. 1965-1980
- Print publication:
- October 2015
-
- Article
- Export citation
SOME QUARTIC DIOPHANTINE EQUATIONS IN THE GAUSSIAN INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 187-194
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
SPECIAL VALUES OF SHIFTED CONVOLUTION DIRICHLET SERIES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 16 June 2015, pp. 47-66
- Print publication:
- 2016
-
- Article
- Export citation
Some applications of modular units
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 03 June 2015, pp. 91-106
-
- Article
- Export citation
Heuristics on pairing-friendly abelian varieties
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 419-443
-
- Article
-
- You have access
- Export citation
Hecke characters associated to Drinfeld modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 2006-2058
- Print publication:
- November 2015
-
- Article
- Export citation
ON THE NON-TRIVIALITY OF THE
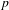 $p$ -ADIC ABEL–JACOBI IMAGE OF GENERALISED HEEGNER CYCLES MODULO
$p$ -ADIC ABEL–JACOBI IMAGE OF GENERALISED HEEGNER CYCLES MODULO 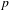 $p$ , II: SHIMURA CURVES
$p$ , II: SHIMURA CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 07 May 2015, pp. 189-222
- Print publication:
- February 2017
-
- Article
- Export citation
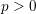
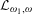
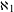
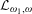
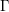
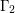
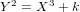

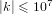
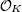 of K. In this paper, we construct
of K. In this paper, we construct 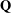
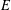
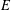
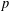
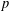
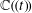
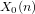

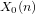


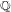
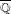


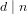

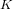


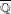

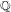
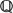
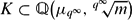
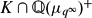
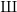
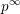
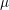
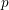
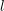
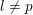
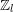

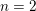
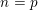
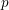
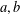

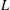
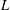
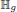 .
.