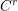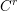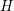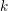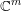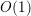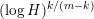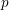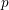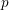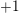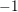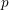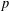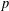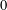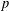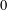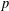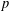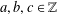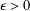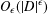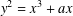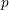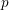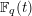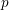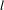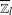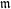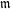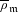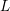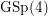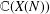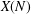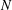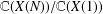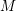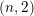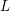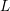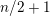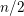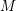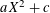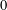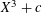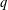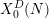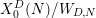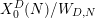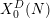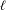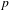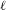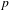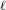Refine listing
Actions for selected content:
539 results in 11Gxx
The Pila–Wilkie theorem for subanalytic families: a complex analytic approach
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 27 July 2017, pp. 2171-2194
- Print publication:
- October 2017
-
- Article
- Export citation
The
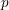 $p$ -adic Gross–Zagier formula on Shimura curves
$p$ -adic Gross–Zagier formula on Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 11 July 2017, pp. 1987-2074
- Print publication:
- October 2017
-
- Article
- Export citation
TRANSPORT PARALLÈLE ET CORRESPONDANCE DE SIMPSON
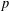 $p$ -ADIQUE
$p$ -ADIQUE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 19 June 2017, e13
-
- Article
-
- You have access
- Open access
- Export citation
A NOTE ON SCHMIDT’S CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 09 June 2017, pp. 191-195
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Non-abelian Cohen–Lenstra heuristics over function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 12 May 2017, pp. 1372-1390
- Print publication:
- July 2017
-
- Article
- Export citation
On descending cohomology geometrically
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 10 May 2017, pp. 1446-1478
- Print publication:
- July 2017
-
- Article
- Export citation
RATIONAL POINTS ON SHIMURA CURVES AND THE MANIN OBSTRUCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 12 April 2017, pp. 144-159
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
Rapoport–Zink spaces for spinor groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 5 / May 2017
- Published online by Cambridge University Press:
- 10 April 2017, pp. 1050-1118
- Print publication:
- May 2017
-
- Article
- Export citation
SUR LA TORSION DANS LA COHOMOLOGIE DES VARIÉTÉS DE SHIMURA DE KOTTWITZ-HARRIS-TAYLOR
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 30 March 2017, pp. 499-517
- Print publication:
- May 2019
-
- Article
- Export citation
On higher regulators of Siegel threefolds II: the connection to the special value
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 5 / May 2017
- Published online by Cambridge University Press:
- 27 March 2017, pp. 889-946
- Print publication:
- May 2017
-
- Article
- Export citation
Construction of ray-class fields by smaller generators and their applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 20 March 2017, pp. 781-812
- Print publication:
- August 2017
-
- Article
- Export citation
NORMAL BASES FOR MODULAR FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 384-392
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Height pairings on orthogonal Shimura varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 474-534
- Print publication:
- March 2017
-
- Article
- Export citation
Picard curves over
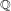 $\mathbb{Q}$ with good reduction away from 3
$\mathbb{Q}$ with good reduction away from 3
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 March 2017, pp. 382-408
-
- Article
-
- You have access
- Export citation
Level structures on abelian varieties and Vojta’s conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 373-394
- Print publication:
- February 2017
-
- Article
- Export citation
MANY CUBIC SURFACES CONTAIN RATIONAL POINTS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 818-839
- Print publication:
- 2017
-
- Article
- Export citation
ITERATION OF QUADRATIC POLYNOMIALS OVER FINITE FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1041-1059
- Print publication:
- 2017
-
- Article
- Export citation
Equations of hyperelliptic Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 1-40
- Print publication:
- January 2017
-
- Article
- Export citation
ON THE COHOMOLOGY OF SOME SIMPLE SHIMURA VARIETIES WITH BAD REDUCTION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 06 December 2016, pp. 1-24
- Print publication:
- January 2019
-
- Article
- Export citation
ON THE
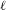 $\ell$-ADIC COHOMOLOGY OF SOME
$\ell$-ADIC COHOMOLOGY OF SOME 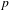 $p$-ADICALLY UNIFORMIZED SHIMURA VARIETIES
$p$-ADICALLY UNIFORMIZED SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 01 December 2016, pp. 1197-1226
- Print publication:
- November 2018
-
- Article
- Export citation