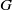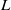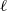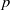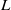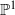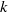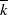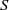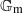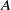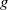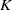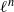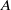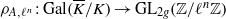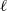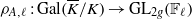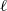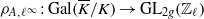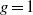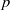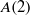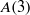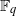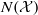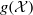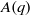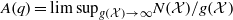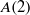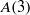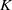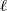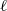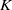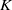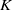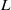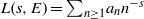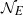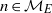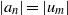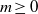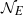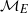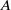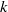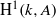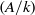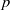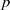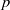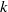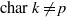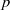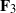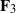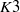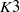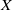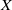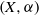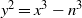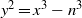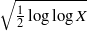Refine listing
Actions for selected content:
539 results in 11Gxx
Comptage des
 $G$-chtoucas: la partie elliptique
$G$-chtoucas: la partie elliptique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 07 October 2013, pp. 2169-2183
- Print publication:
- December 2013
-
- Article
- Export citation
Trivial zeros of
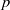 $p$ -adic
$p$ -adic 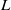 $L$ -functions at near-central points
$L$ -functions at near-central points
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 24 September 2013, pp. 561-598
- Print publication:
- July 2014
-
- Article
- Export citation
SPECIAL CURVES AND POSTCRITICALLY FINITE POLYNOMIALS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 1 / 2013
- Published online by Cambridge University Press:
- 19 September 2013, e3
-
- Article
-
- You have access
- Open access
- Export citation
Integral division points on curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 09 September 2013, pp. 2011-2035
- Print publication:
- December 2013
-
- Article
- Export citation
Modular subgroups, dessins d’enfants and elliptic K3 surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 271-318
-
- Article
-
- You have access
- Export citation
Determinants of subquotients of Galois representations associated with abelian varieties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 517-559
- Print publication:
- July 2014
-
- Article
- Export citation
On the arithmetic fundamental lemma in the minuscule case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 10 / October 2013
- Published online by Cambridge University Press:
- 04 July 2013, pp. 1631-1666
- Print publication:
- October 2013
-
- Article
- Export citation
On lower bounds for the Ihara constants
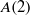 $A(2)$ and
$A(2)$ and 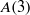 $A(3)$
$A(3)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 03 May 2013, pp. 1108-1128
- Print publication:
- July 2013
-
- Article
- Export citation
Independence of
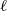 $\ell $-adic Galois representations over function fields
$\ell $-adic Galois representations over function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 25 April 2013, pp. 1091-1107
- Print publication:
- July 2013
-
- Article
- Export citation
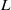 $L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
$L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 22 March 2013, pp. 509-519
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Weil–Châtelet divisible elements in Tate–Shafarevich groups I: The Bashmakov problem for elliptic curves over
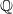 $ \mathbb{Q} $
$ \mathbb{Q} $
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 729-753
- Print publication:
- May 2013
-
- Article
- Export citation
The André–Oort conjecture for Drinfeld modular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 507-567
- Print publication:
- April 2013
-
- Article
- Export citation
Random Dieudonné modules, random
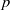 $p$-divisible groups, and random curves over finite fields
$p$-divisible groups, and random curves over finite fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 13 February 2013, pp. 651-676
- Print publication:
- July 2013
-
- Article
- Export citation
Failure of the Hasse principle on general
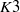 $K 3$ surfaces
$K 3$ surfaces
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 08 February 2013, pp. 853-877
- Print publication:
- October 2013
-
- Article
- Export citation
ON SELMER GROUPS OF QUADRATIC TWISTS OF ELLIPTIC CURVES WITH A TWO-TORSION OVER
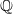 $\mathbb {Q}$
$\mathbb {Q}$
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 15 January 2013, pp. 303-319
- Print publication:
- July 2013
-
- Article
- Export citation
Dihedral Iwasawa theory of nearly ordinary quaternionic automorphic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 13 December 2012, pp. 356-416
- Print publication:
- March 2013
-
- Article
- Export citation
The André–Oort conjecture for the moduli space of abelian surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 2 / February 2013
- Published online by Cambridge University Press:
- 11 December 2012, pp. 204-216
- Print publication:
- February 2013
-
- Article
- Export citation
Differential equations and expansions for quaternionic modular forms in the discriminant 6 case
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 December 2012, pp. 385-399
-
- Article
-
- You have access
- Export citation
Elliptic curves with a given number of points over finite fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 2 / February 2013
- Published online by Cambridge University Press:
- 01 November 2012, pp. 175-203
- Print publication:
- February 2013
-
- Article
- Export citation
Schwarzian differential equations and Hecke eigenforms on Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 31 October 2012, pp. 1-31
- Print publication:
- January 2013
-
- Article
- Export citation