Refine listing
Actions for selected content:
539 results in 11Gxx
ELEMENTS OF LARGE ORDER IN PRIME FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 16 October 2012, pp. 169-176
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
Critically separable rational maps in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 12 October 2012, pp. 1880-1896
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
Lifting, restricting and sifting integral points on affine homogeneous varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 11 October 2012, pp. 1695-1716
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
Identifying supersingular elliptic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 317-325
-
- Article
-
- You have access
- Export citation
Complete addition laws on abelian varieties
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 308-316
-
- Article
-
- You have access
- Export citation
Accelerating the CM method
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 August 2012, pp. 172-204
-
- Article
-
- You have access
- Export citation
Sato–Tate distributions and Galois endomorphism modules in genus 2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 25 July 2012, pp. 1390-1442
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Descent obstructions and Brauer–Manin obstruction in positive characteristic
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 01 June 2012, pp. 545-551
- Print publication:
- July 2013
-
- Article
- Export citation
CM cycles on Shimura curves, and p-adic L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 15 May 2012, pp. 1003-1032
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
On the equations a2−2b6=cp and a2−2=cp
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 May 2012, pp. 158-171
-
- Article
-
- You have access
- Export citation
ON SELMER GROUPS AND TATE–SHAFAREVICH GROUPS FOR ELLIPTIC CURVES y2=x3−n3
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 236-274
- Print publication:
- July 2012
-
- Article
- Export citation
ON THE DISTRIBUTION OF TORSION POINTS MODULO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 339-347
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Higher-level canonical subgroups for p-divisible groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 13 December 2011, pp. 363-419
- Print publication:
- April 2012
-
- Article
- Export citation
Symmetry and parity in Frobenius action on cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 08 December 2011, pp. 295-303
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Proving the Birch and Swinnerton-Dyer conjecture for specific elliptic curves of analytic rank zero and one
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 November 2011, pp. 327-350
-
- Article
-
- You have access
- Export citation
ON THE DISTRIBUTION OF GALOIS GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 21 October 2011, pp. 35-44
- Print publication:
- January 2012
-
- Article
- Export citation
Cohomologie d’intersection des variétés modulaires de Siegel, suite
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 28 September 2011, pp. 1671-1740
- Print publication:
- November 2011
-
- Article
-
- You have access
- Export citation
Some unlikely intersections beyond André–Oort
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 30 August 2011, pp. 1-27
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Families of explicitly isogenous Jacobians of variable-separated curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 179-199
-
- Article
-
- You have access
- Export citation
Computations with classical and p-adic modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 214-231
-
- Article
-
- You have access
- Export citation
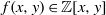
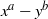
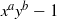
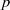
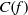
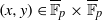
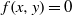
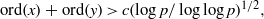

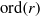

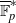
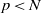
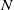
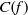
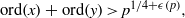
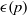
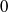
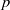
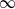
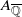 (the
(the 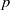
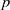
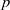
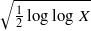 as
as 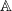 be a commutative algebraic group defined over a number field
be a commutative algebraic group defined over a number field 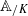 , we determine the average values of
, we determine the average values of 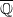 . Finally, we formulate and prove a variant of the Mordell–Lang conjecture for subvarieties of
. Finally, we formulate and prove a variant of the Mordell–Lang conjecture for subvarieties of 