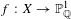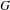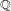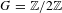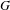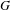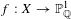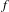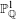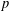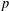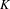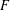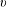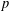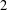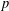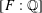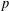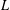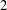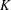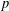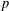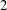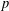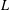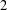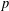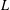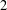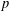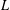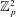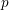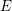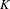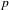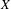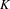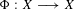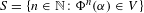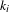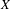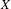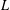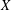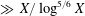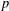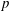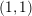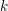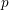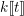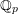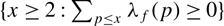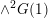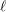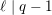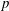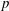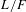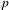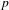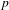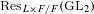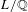Refine listing
Actions for selected content:
539 results in 11Gxx
DENSITY RESULTS FOR SPECIALIZATION SETS OF GALOIS COVERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 25 October 2019, pp. 1455-1496
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
Compatible systems and ramification
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 21 October 2019, pp. 2334-2353
- Print publication:
- December 2019
-
- Article
- Export citation
EISENSTEIN–KRONECKER SERIES VIA THE POINCARÉ BUNDLE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 30 September 2019, e34
-
- Article
-
- You have access
- Open access
- Export citation
RIGIDITY FOR RIGID ANALYTIC MOTIVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 27 September 2019, pp. 1341-1369
- Print publication:
- July 2021
-
- Article
- Export citation
THE EXPLICIT MORDELL CONJECTURE FOR FAMILIES OF CURVES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 19 September 2019, e31
-
- Article
-
- You have access
- Open access
- Export citation
TATE’S CONJECTURE AND THE TATE–SHAFAREVICH GROUP OVER GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 17 September 2019, pp. 1001-1022
- Print publication:
- May 2021
-
- Article
- Export citation
PARALLEL WEIGHT 2 POINTS ON HILBERT MODULAR EIGENVARIETIES AND THE PARITY CONJECTURE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 04 September 2019, e27
-
- Article
-
- You have access
- Open access
- Export citation
CODIMENSION TWO CYCLES IN IWASAWA THEORY AND ELLIPTIC CURVES WITH SUPERSINGULAR REDUCTION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 August 2019, e25
-
- Article
-
- You have access
- Open access
- Export citation
ON THE EULER CHARACTERISTICS OF SIGNED SELMER GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 09 July 2019, pp. 238-246
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Families of Picard modular forms and an application to the Bloch–Kato conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 25 June 2019, pp. 1327-1401
- Print publication:
- July 2019
-
- Article
- Export citation
THE DYNAMICAL MORDELL–LANG CONJECTURE FOR ENDOMORPHISMS OF SEMIABELIAN VARIETIES DEFINED OVER FIELDS OF POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 24 June 2019, pp. 669-698
- Print publication:
- March 2021
-
- Article
- Export citation
ON A NONCRITICAL SYMMETRIC SQUARE
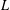 $L$-VALUE OF THE CONGRUENT NUMBER ELLIPTIC CURVES
$L$-VALUE OF THE CONGRUENT NUMBER ELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 27 May 2019, pp. 13-22
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
ENLARGED MIXED SHIMURA VARIETIES, BI-ALGEBRAIC SYSTEM AND SOME AX TYPE TRANSCENDENTAL RESULTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 27 May 2019, e16
-
- Article
-
- You have access
- Open access
- Export citation
GOLDFELD’S CONJECTURE AND CONGRUENCES BETWEEN HEEGNER POINTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 27 May 2019, e15
-
- Article
-
- You have access
- Open access
- Export citation
On Some Generalized Rapoport–Zink Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 03 May 2019, pp. 1111-1187
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Cycle classes in overconvergent rigid cohomology and a semistable Lefschetz
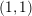 $(1,1)$ theorem
$(1,1)$ theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 02 May 2019, pp. 1025-1045
- Print publication:
- May 2019
-
- Article
- Export citation
Chebyshev’s bias for analytic L-functions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 22 March 2019, pp. 103-140
- Print publication:
- July 2020
-
- Article
- Export citation
Cohen–Lenstra heuristics for étale group schemes and symplectic pairings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 4 / April 2019
- Published online by Cambridge University Press:
- 20 March 2019, pp. 758-775
- Print publication:
- April 2019
-
- Article
- Export citation
Local Shtukas and Divisible Local Anderson Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1163-1207
- Print publication:
- October 2019
-
- Article
-
- You have access
- Open access
- Export citation
TWISTED TRIPLE PRODUCT
 $\text{p}$-ADIC L-FUNCTIONS AND HIRZEBRUCH–ZAGIER CYCLES
$\text{p}$-ADIC L-FUNCTIONS AND HIRZEBRUCH–ZAGIER CYCLES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 20 February 2019, pp. 1947-1992
- Print publication:
- November 2020
-
- Article
- Export citation