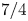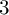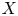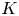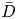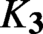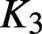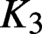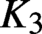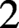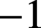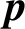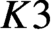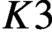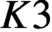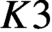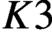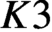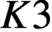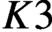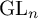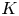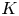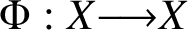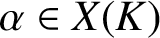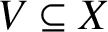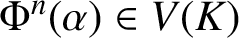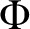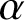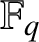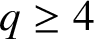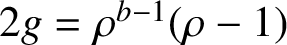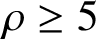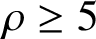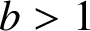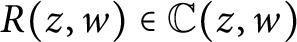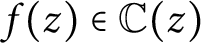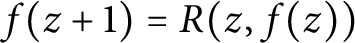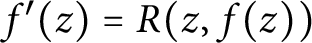Refine listing
Actions for selected content:
539 results in 11Gxx
Large families of elliptic curves ordered by conductor
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 22 June 2021, pp. 1538-1583
- Print publication:
- July 2021
-
- Article
- Export citation
GEOMETRIC QUADRATIC CHABAUTY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 17 June 2021, pp. 279-333
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
Successive minima and asymptotic slopes in Arakelov geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1302-1339
- Print publication:
- June 2021
-
- Article
- Export citation
Hyperbolic tessellations and generators of
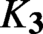 ${K}_{\textbf {3}}$ for imaginary quadratic fields
${K}_{\textbf {3}}$ for imaginary quadratic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 24 May 2021, e40
-
- Article
-
- You have access
- Open access
- Export citation
ELLIPTIC CURVES AND
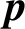 $\boldsymbol {p}$-ADIC ELLIPTIC TRANSCENDENCE
$\boldsymbol {p}$-ADIC ELLIPTIC TRANSCENDENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 21 May 2021, pp. 31-36
- Print publication:
- February 2022
-
- Article
- Export citation
The effective Shafarevich conjecture for abelian varieties of
 ${\text {GL}_{2}}$-type
${\text {GL}_{2}}$-type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 19 May 2021, e39
-
- Article
-
- You have access
- Open access
- Export citation
On the cohomology of Kobayashi’s plus/minus norm groups and applications
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 1-24
- Print publication:
- July 2022
-
- Article
- Export citation
Cyclicity of elliptic curves modulo primes in arithmetic progressions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 1277-1309
- Print publication:
- October 2022
-
- Article
- Export citation
Singular units and isogenies between CM elliptic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 1022-1035
- Print publication:
- May 2021
-
- Article
- Export citation
CM liftings of
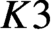 $K3$ surfaces over finite fields and their applications to the Tate conjecture
$K3$ surfaces over finite fields and their applications to the Tate conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 April 2021, e29
-
- Article
-
- You have access
- Open access
- Export citation
HECKE OPERATORS AND THE COHERENT COHOMOLOGY OF SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 April 2021, pp. 1-69
- Print publication:
- January 2023
-
- Article
- Export citation
The strong Suslin reciprocity law
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 01 April 2021, pp. 649-676
- Print publication:
- April 2021
-
- Article
- Export citation
SPECIAL VALUES OF THE ZETA FUNCTION OF AN ARITHMETIC SURFACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 15 March 2021, pp. 2043-2091
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
Extending tamely ramified strict 1-motives into két log 1-motives
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 09 March 2021, e20
-
- Article
-
- You have access
- Open access
- Export citation
Dynamical and arithmetic degrees for random iterations of maps on projective space
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 26 February 2021, pp. 369-385
- Print publication:
- September 2021
-
- Article
- Export citation
A SPARSITY RESULT FOR THE DYNAMICAL MORDELL–LANG CONJECTURE IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 23 February 2021, pp. 381-390
- Print publication:
- December 2021
-
- Article
- Export citation
CHARACTERISTIC POLYNOMIALS OF SIMPLE ORDINARY ABELIAN VARIETIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 391-397
- Print publication:
- December 2021
-
- Article
- Export citation
Effective finiteness of solutions to certain differential and difference equations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 16 February 2021, pp. 52-67
- Print publication:
- March 2022
-
- Article
- Export citation
IHARA LEMMA AND LEVEL RAISING IN HIGHER DIMENSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 1701-1726
- Print publication:
- September 2022
-
- Article
- Export citation
EXTREMAL CASES OF RAPOPORT–ZINK SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 20 January 2021, pp. 1727-1782
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- Export citation