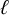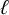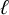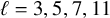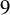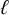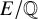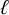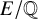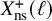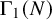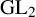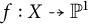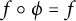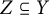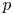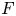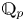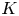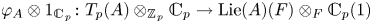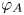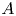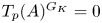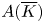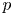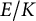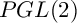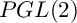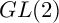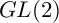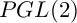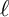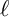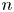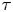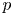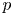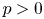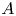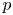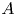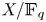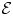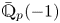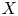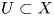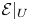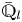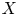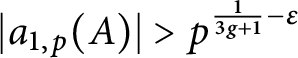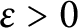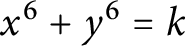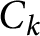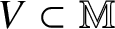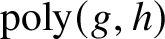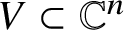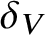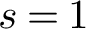Refine listing
Actions for selected content:
539 results in 11Gxx
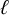 $\ell $-adic images of Galois for elliptic curves over
$\ell $-adic images of Galois for elliptic curves over  $\mathbb {Q}$ (and an appendix with John Voight)
$\mathbb {Q}$ (and an appendix with John Voight)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 August 2022, e62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A conjecture strengthening the Zariski dense orbit problem for birational maps of dynamical degree one
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 07 July 2022, pp. 477-491
- Print publication:
- June 2023
-
- Article
- Export citation
On p-adic uniformization of abelian varieties with good reduction
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1449-1476
- Print publication:
- July 2022
-
- Article
- Export citation
Some cases of Kudla’s modularity conjecture for unitary Shimura varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On elliptic curves with p-isogenies over quadratic fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 07 June 2022, pp. 945-964
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SELMER GROUPS OF ELLIPTIC CURVES OVER THE
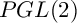 $PGL(2)$ EXTENSION
$PGL(2)$ EXTENSION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 922-938
- Print publication:
- December 2022
-
- Article
- Export citation
THE BOUNDARY OF THE p-RANK
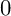 $0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
$0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 865-887
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tropical moments of tropical Jacobians
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 May 2022, pp. 1045-1075
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion points on isogenous abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 20 July 2022, pp. 1020-1051
- Print publication:
- May 2022
-
- Article
- Export citation
Effective rigid analytic trivializations for Drinfeld modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 20 April 2022, pp. 713-742
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the algebraicity about the Hodge numbers of the Hilbert schemes of algebraic surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 392-403
-
- Article
- Export citation
Regular integral models for Shimura varieties of orthogonal type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 831-867
- Print publication:
- April 2022
-
- Article
- Export citation
Reductions of abelian surfaces over global function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 16 June 2022, pp. 893-950
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rank 2 local systems and abelian varieties II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 868-892
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds for the distribution of the Frobenius traces associated to products of non-CM elliptic curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 07 March 2022, pp. 687-712
- Print publication:
- June 2023
-
- Article
- Export citation
Integers that are sums of two rational sixth powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 07 March 2022, pp. 166-177
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Point counting for foliations over number fields
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 March 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chow groups and L-derivatives of automorphic motives for unitary groups, II.
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 March 2022, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On monic abelian cubics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 16 May 2022, pp. 550-567
- Print publication:
- March 2022
-
- Article
- Export citation
VALUES OF ZETA FUNCTIONS OF ARITHMETIC SURFACES AT
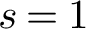 $s=1$
$s=1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 28 February 2022, pp. 2455-2496
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation