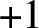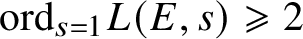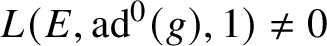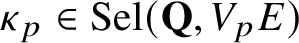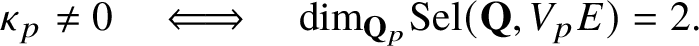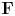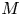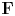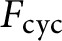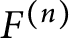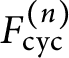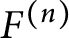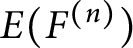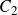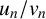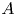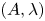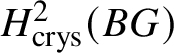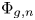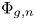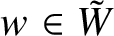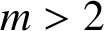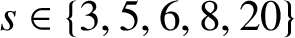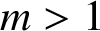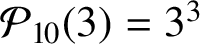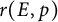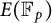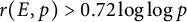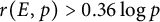Refine listing
Actions for selected content:
539 results in 11Gxx
ON THE GEOMETRY OF THE PAPPAS–RAPOPORT MODELS FOR PEL SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 18 February 2022, pp. 2403-2445
- Print publication:
- September 2023
-
- Article
- Export citation
INDIVISIBILITY OF HEEGNER CYCLES OVER SHIMURA CURVES AND SELMER GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 2297-2336
- Print publication:
- September 2023
-
- Article
- Export citation
On the nonvanishing of generalised Kato classes for elliptic curves of rank 2
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 February 2022, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE p-ADIC GROSS–ZAGIER FORMULA ON SHIMURA CURVES, II: NONSPLIT PRIMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 2199-2240
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The monodromy of unit-root F-isocrystals with geometric origin
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 18 April 2022, pp. 334-365
- Print publication:
- February 2022
-
- Article
- Export citation
Torsion properties of modified diagonal classes on triple products of modular curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 31 January 2022, pp. 68-86
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic growth of Mordell–Weil ranks of elliptic curves in noncommutative towers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 31 January 2022, pp. 1050-1062
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wild Galois representations: a family of hyperelliptic curves with large inertia image
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 619-633
- Print publication:
- November 2022
-
- Article
- Export citation
APÉRY LIMITS FOR ELLIPTIC
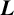 $\boldsymbol {L}$-VALUES
$\boldsymbol {L}$-VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 273-279
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Faltings height and Néron–Tate height of a theta divisor
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 1-32
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dieudonné theory via cohomology of classifying stacks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 15 December 2021, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum: Generic rank of Betti map and unlikely intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 05 January 2022, pp. 2747-2748
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
NOTES ON THE DPRM PROPERTY FOR LISTABLE STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 23 November 2021, pp. 273-312
- Print publication:
- March 2022
-
- Article
- Export citation
The essential dimension of congruence covers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 27 October 2021, pp. 2407-2432
- Print publication:
- November 2021
-
- Article
- Export citation
Congruences for critical values of higher derivatives of twisted Hasse–Weil L-functions, III
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 19 October 2021, pp. 431-456
- Print publication:
- September 2022
-
- Article
- Export citation
AUTOMORPHIC LEFSCHETZ PROPERTIES FOR NONCOMPACT ARITHMETIC MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 1655-1702
- Print publication:
- July 2023
-
- Article
- Export citation
Cordial elements and dimensions of affine Deligne–Lusztig varieties
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 September 2021, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A UNIQUE PERFECT POWER DECAGONAL NUMBER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 06 August 2021, pp. 212-216
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE GENERIC FIBRE OF MODULI SPACES OF BOUNDED LOCAL G-SHTUKAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 July 2021, pp. 799-878
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An elliptic curve analogue of Pillai’s lower bound on primitive roots
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 496-505
- Print publication:
- June 2022
-
- Article
- Export citation