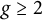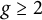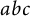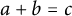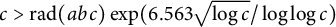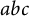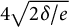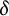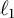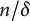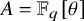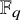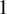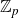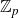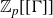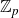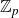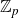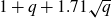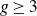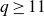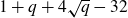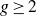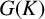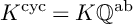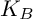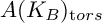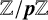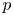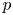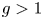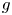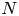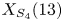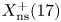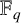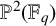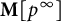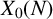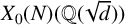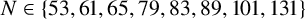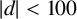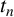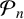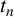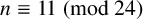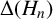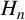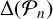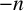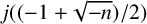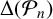Refine listing
Actions for selected content:
545 results in 11Gxx
Isogeny graphs on superspecial abelian varieties: eigenvalues and connection to Bruhat–Tits buildings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 1891-1916
- Print publication:
- December 2024
-
- Article
- Export citation
A new lower bound in the
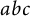 $abc$ conjecture
$abc$ conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 369-378
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic relations among Goss’s zeta values on elliptic curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e90
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hensel minimality II: Mixed characteristic and a diophantine application
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structure of fine Selmer groups over
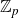 $\mathbb{Z}_{p}$-extensions
$\mathbb{Z}_{p}$-extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 04 October 2023, pp. 287-308
- Print publication:
- March 2024
-
- Article
- Export citation
Lower bounds on the maximal number of rational points on curves over finite fields
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 213-238
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE MORDELL–LANG CONJECTURE FOR SEMIABELIAN VARIETIES DEFINED OVER FIELDS OF POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 254-264
- Print publication:
- April 2024
-
- Article
- Export citation
Hodge classes and the Jacquet–Langlands correspondence
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 September 2023, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ESSENTIAL TORSION FINITENESS OF ABELIAN VARIETIES OVER TORSION FIELDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 91-127
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Connected components of affine Deligne–Lusztig varieties for unramified groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 17 August 2023, pp. 2051-2088
- Print publication:
- October 2023
-
- Article
- Export citation
Kudla–Rapoport conjecture for Krämer models
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1673-1740
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RANK JUMPS AND GROWTH OF SHAFAREVICH–TATE GROUPS FOR ELLIPTIC CURVES IN
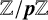 ${\mathbb {Z}}/\boldsymbol{p}{\mathbb {Z}}$-EXTENSIONS
${\mathbb {Z}}/\boldsymbol{p}{\mathbb {Z}}$-EXTENSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
p-adic Eichler–Shimura maps for the modular curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1214-1249
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quadratic Chabauty for modular curves: algorithms and examples
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1111-1152
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TANGENT-FILLING PLANE CURVES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 02 May 2023, pp. 301-315
- Print publication:
- April 2024
-
- Article
- Export citation
Zariski dense orbits for regular self-maps of split semiabelian varieties in positive characteristic
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 479-519
- Print publication:
- November 2023
-
- Article
- Export citation
Log p-divisible groups associated with log 1-motives
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 28 April 2023, pp. 946-983
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPUTING POINTS ON BIELLIPTIC MODULAR CURVES OVER FIXED QUADRATIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 20 April 2023, pp. 6-13
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON DISCRIMINANTS OF MINIMAL POLYNOMIALS OF THE RAMANUJAN
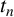 $t_n$ CLASS INVARIANTS
$t_n$ CLASS INVARIANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 264-275
- Print publication:
- October 2023
-
- Article
- Export citation
Algebraicity of L-values attached to quaternionic modular forms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 30 March 2023, pp. 638-679
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation