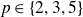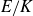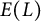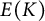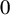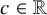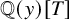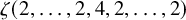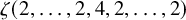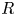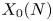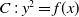Refine listing
Actions for selected content:
539 results in 11Gxx
DECOMPOSITION OF THE JACOBIAN OF SOME TWISTS OF A GENUS
 $2$ CURVE
$2$ CURVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 445-459
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THEOREM OF WARD ON SYMMETRIES OF ELLIPTIC NETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 93-106
- Print publication:
- February 2025
-
- Article
- Export citation
Sharp bounds on the height of K-semistable Fano varieties I, the toric case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 10 October 2024, pp. 2366-2406
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the integral part of A-motivic cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 16 September 2024, pp. 1715-1783
- Print publication:
- August 2024
-
- Article
- Export citation
Tropical curves in abelian surfaces I: enumeration of curves passing through points
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 109-148
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Failure of Galois Descent for p-Selmer Groups of Elliptic Curves
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 185-218
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal subfields of elliptic curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1029-1045
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Heisenberg covering of the Fermat curve
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1637-1663
- Print publication:
- October 2025
-
- Article
- Export citation
NORMAL BASES FOR FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 44-55
- Print publication:
- August 2024
-
- Article
- Export citation
Attractors are not algebraic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1073-1100
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KOBAYASHI-OCHIAI’S FINITENESS THEOREM FOR ORBIFOLD PAIRS OF GENERAL TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 17 April 2024, pp. 2713-2732
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Affine Bruhat order and Demazure products
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 April 2024, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lower Bounds for the Canonical Height of a Unicritical Polynomial and Capacity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Evaluation of
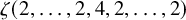 $ \zeta (2,\ldots ,2,4,2,\ldots ,2) $ and period polynomial relations
$ \zeta (2,\ldots ,2,4,2,\ldots ,2) $ and period polynomial relations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modular curves and Néron models of generalized Jacobians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 26 March 2024, pp. 945-981
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Models and integral differentials of hyperelliptic curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 18 March 2024, pp. 382-439
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WEIERSTRASS ZETA FUNCTIONS AND p-ADIC LINEAR RELATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 11 March 2024, pp. 234-243
- Print publication:
- October 2024
-
- Article
- Export citation
Constructing abelian varieties from rank 2 Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 709-731
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How to solve a binary cubic equation in integers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 609-624
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
There are at most finitely many singular moduli that are S-units
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 732-770
- Print publication:
- April 2024
-
- Article
- Export citation