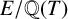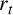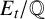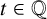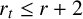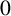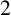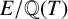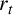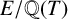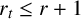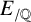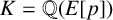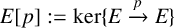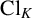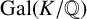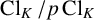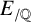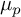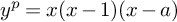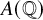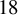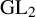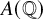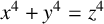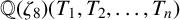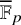Refine listing
Actions for selected content:
539 results in 11Gxx
Canonical heights for abelian group actions of maximal dynamical rank
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 January 2025, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A single source theorem for primitive points on curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN UPPER BOUND FOR THE GENERALISED GREATEST COMMON DIVISOR OF RATIONAL POINTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 248-253
- Print publication:
- October 2025
-
- Article
- Export citation
Control theorems for Hilbert modular varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 14 January 2025, pp. 530-549
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOW RANK SPECIALISATIONS OF ELLIPTIC SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 118-127
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The isotrivial case in the Mordell-Lang conjecture for semiabelian varieties defined over fields of positive characteristic
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 461-476
- Print publication:
- June 2025
-
- Article
- Export citation
Chai's conjecture for semiabelian Jacobians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 120-147
- Print publication:
- January 2025
-
- Article
- Export citation
A classification of Shimura curves in
 $ \mathscr {A}_g$
$ \mathscr {A}_g$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOWER BOUNDS FOR THE MAHLER MEASURE AND INERTIA DEGREES OF PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 106-117
- Print publication:
- August 2025
-
- Article
- Export citation
SOME CASES OF OORT’S CONJECTURE ABOUT NEWTON POLYGONS OF CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 93-103
- Print publication:
- March 2025
-
- Article
- Export citation
CLASS GROUP STATISTICS FOR TORSION FIELDS GENERATED BY ELLIPTIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 245-264
- Print publication:
- April 2025
-
- Article
- Export citation
ARBITRARILY LARGE p-TORSION IN TATE-SHAFAREVICH GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 November 2024, pp. 481-502
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ODA’S PROBLEM AND SPECIAL LOCI
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 November 2024, pp. 503-539
- Print publication:
- March 2025
-
- Article
- Export citation
Rational torsion points on abelian surfaces with quaternionic multiplication
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 November 2024, e92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POINTS ON
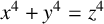 $x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF
$x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF 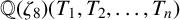 ${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 November 2024, pp. 19-31
- Print publication:
- February 2025
-
- Article
- Export citation
Mod p points on shimura varieties of parahoric level
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Height functions on Hecke orbits and the generalised André–Pink–Zannier conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2531-2584
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computing the Cassels–Tate pairing for genus two jacobians with rational two-torsion points
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 3 / November 2024
- Published online by Cambridge University Press:
- 06 December 2024, pp. 415-437
- Print publication:
- November 2024
-
- Article
- Export citation
Local monodromy of Drinfeld modules
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 03 December 2024, pp. 2656-2683
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zagier–Hoffman’s Conjectures in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 22 October 2024, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation