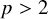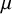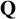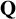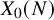Refine listing
Actions for selected content:
539 results in 11Gxx
The p-adic limits of class numbers in
 ${\mathbb{Z}}_p$-towers
${\mathbb{Z}}_p$-towers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 23 May 2025, pp. 299-329
- Print publication:
- September 2025
-
- Article
- Export citation
Canonical integral models for Shimura varieties of abelian type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 April 2025, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ordinary isogeny graphs with level structure
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 March 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformation theory for prismatic G-displays
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 21 March 2025, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rationality and arithmetic of the moduli of abelian varieties
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOMBRE DE PETITS POINTS SUR UNE VARIÉTÉ ABÉLIENNE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 705-761
- Print publication:
- May 2025
-
- Article
- Export citation
Deformations of Theta Integrals and A Conjecture of Gross-Zagier
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 March 2025, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A linear AFL for quaternion algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1-23
-
- Article
- Export citation
Geometric local systems on the projective line minus four points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 01 July 2025, pp. 536-554
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kodaira–Spencer isomorphisms and degeneracy maps on Iwahori-level Hilbert modular varieties: the saving trace
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 February 2025, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theory of heat equations for sigma functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 February 2025, pp. 365-422
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert’s 10th problem via Mordell curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 939-949
- Print publication:
- September 2025
-
- Article
- Export citation
On the
 $\mu$-invariant of two-variable
$\mu$-invariant of two-variable  $2$-adic
$2$-adic  $\boldsymbol{L}$-functions
$\boldsymbol{L}$-functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 325-355
- Print publication:
- September 2025
-
- Article
- Export citation
Reduction of bielliptic surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 12 February 2025, pp. 856-873
- Print publication:
- September 2025
-
- Article
- Export citation
Average Analytic Ranks of Elliptic Curves over Number Fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 February 2025, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE COHOMOLOGY OF p-ADIC DELIGNE-LUSZTIG SCHEMES OF COXETER TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1429-1462
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the L-polynomials of curves over finite fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON PSEUDO-NULLITY OF THE FINE MORDELL–WEIL GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 71-79
- Print publication:
- August 2025
-
- Article
- Export citation
On the linear AFL: the non-basic case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 23 June 2025, pp. 385-425
- Print publication:
- February 2025
-
- Article
- Export citation
Complete verification of strong BSD for many modular abelian surfaces over
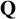 ${\mathbf {Q}}$
${\mathbf {Q}}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 January 2025, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation