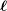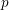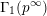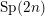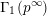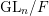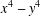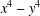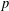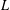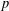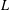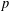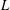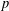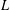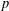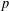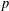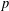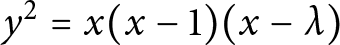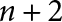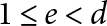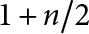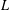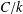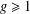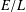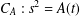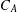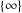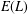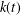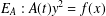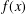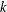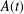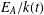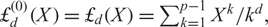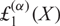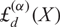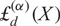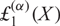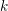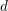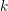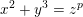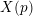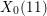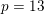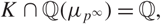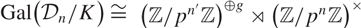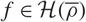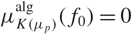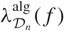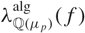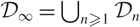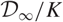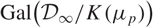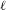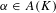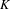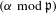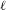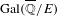Refine listing
Actions for selected content:
539 results in 11Gxx
Corrigendum: Around
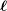 $\boldsymbol{\ell }$-independence
$\boldsymbol{\ell }$-independence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 29 May 2020, pp. 1262-1274
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
Shimura varieties at level
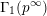 $\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations
$\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 26 May 2020, pp. 1152-1230
- Print publication:
- June 2020
-
- Article
- Export citation
INTEGERS REPRESENTED BY
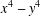 $x^{4}-y^{4}$ REVISITED
$x^{4}-y^{4}$ REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 38-49
- Print publication:
- February 2021
-
- Article
- Export citation
The size of the primes obstructing the existence of rational points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 652-704
- Print publication:
- April 2021
-
- Article
- Export citation
Möbius Randomness Law for Frobenius Traces of Ordinary Curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 192-203
- Print publication:
- March 2021
-
- Article
- Export citation
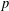 $p$-ADIC
$p$-ADIC 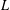 $L$-FUNCTIONS FOR UNITARY GROUPS
$L$-FUNCTIONS FOR UNITARY GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 May 2020, e9
-
- Article
-
- You have access
- Open access
- Export citation
Semistable models of elliptic curves over residue characteristic 2
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 29 April 2020, pp. 154-162
- Print publication:
- March 2021
-
- Article
- Export citation
The Modularity of Special Cycles on Orthogonal Shimura Varieties over Totally Real Fields under the Beilinson–Bloch Conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 30 March 2020, pp. 39-53
- Print publication:
- March 2021
-
- Article
- Export citation
ON INTEGRAL POINTS ON ISOTRIVIAL ELLIPTIC CURVES OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 27 March 2020, pp. 177-185
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
RELATIVE UNITARY RZ-SPACES AND THE ARITHMETIC FUNDAMENTAL LEMMA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 March 2020, pp. 241-301
- Print publication:
- January 2022
-
- Article
- Export citation
GENERALIZED FINITE POLYLOGARITHMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 19 February 2020, pp. 66-80
- Print publication:
- January 2021
-
- Article
- Export citation
Gonality of dynatomic curves and strong uniform boundedness of preperiodic points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 17 February 2020, pp. 733-743
- Print publication:
- April 2020
-
- Article
- Export citation
Generalized Beilinson Elements and Generalized Soulé Characters
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 06 February 2020, pp. 542-571
- Print publication:
- April 2021
-
- Article
- Export citation
Ordinary primes in Hilbert modular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 06 February 2020, pp. 647-678
- Print publication:
- April 2020
-
- Article
- Export citation
Belyi’s theorem in characteristic two
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 2 / February 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 325-339
- Print publication:
- February 2020
-
- Article
- Export citation
FINE DELIGNE–LUSZTIG VARIETIES AND ARITHMETIC FUNDAMENTAL LEMMAS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 10 December 2019, e47
-
- Article
-
- You have access
- Open access
- Export citation
The generalized Fermat equation with exponents 2, 3,
 $n$
$n$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 77-113
- Print publication:
- January 2020
-
- Article
- Export citation
Variation of the algebraic λ-invariant over a solvable extension
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 21 November 2019, pp. 499-521
- Print publication:
- May 2021
-
- Article
- Export citation
REDUCTIONS OF POINTS ON ALGEBRAIC GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 14 November 2019, pp. 1637-1669
- Print publication:
- September 2021
-
- Article
- Export citation
GALOIS CONJUGATES OF SPECIAL POINTS AND SPECIAL SUBVARIETIES IN SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 30 October 2019, pp. 1075-1089
- Print publication:
- May 2021
-
- Article
- Export citation