Refine listing
Actions for selected content:
364 results in 11Rxx
Determining Fitting ideals of minus class groups via the equivariant Tamagawa number conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1399-1426
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
On number fields with given ramification
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1359-1373
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
A Dirichlet series expansion for the p-adic zeta-function
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 215-224
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
Zeta functions of twisted modular curves
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 89-103
- Print publication:
- February 2006
-
- Article
-
- You have access
- Export citation
On Units and Class Numbers of Pure Cubic Fields
- Part of
-
- Journal:
- Mathematika / Volume 52 / Issue 1-2 / December 2005
- Published online by Cambridge University Press:
- 21 December 2009, pp. 87-91
- Print publication:
- December 2005
-
- Article
- Export citation
The distribution of the irreducibles in an algebraic number field
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-390
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Class number formulae in the form of a product of determinants in function fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 227-238
- Print publication:
- April 2005
-
- Article
-
- You have access
- Export citation
The values of Mahler measures
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-148
- Print publication:
- December 2004
-
- Article
- Export citation
Counting points of bounded relative height
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-152
- Print publication:
- December 2003
-
- Article
- Export citation
The Hooley–Huxley contour method, for problems in number fields II: factorization and divisibility
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 201-225
- Print publication:
- June 2002
-
- Article
- Export citation
Character sums and the series L(1, χ)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-436
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
Bases for cyclotomic units over function fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 56-70
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
Uniformity over primes of unramified splittings
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 177-189
- Print publication:
- June 1998
-
- Article
- Export citation
An extension theorem for integral representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-15
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
genus theory for function fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 3 / June 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-310
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation
Relative norms of prime ideals in small regions
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 40-62
- Print publication:
- June 1996
-
- Article
- Export citation
Bounding a unit index in terms of a ring index
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 199-205
- Print publication:
- June 1995
-
- Article
- Export citation
A variant of Moore's uniqueness of reciprocity laws
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 246-255
- Print publication:
- December 1993
-
- Article
- Export citation
On Mahler's compound bodies
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-215
- Print publication:
- October 1993
-
- Article
-
- You have access
- Export citation
The spatial distribution of algebraic integers on constant-norm hypersurfaces
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 350-366
- Print publication:
- December 1992
-
- Article
- Export citation
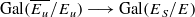 are injective. We discuss generalizations of this result.
are injective. We discuss generalizations of this result.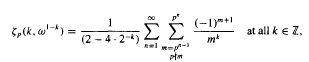 Where the convergence of the first summation is for the
Where the convergence of the first summation is for the 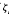
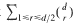 with all its roots lying in the Galois closure
with all its roots lying in the Galois closure 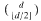 over ℚ This is used to show that some numbers considered earlier by Boyd are not Mahler measures. The set of numbers which occur as Mahler measures of both reciprocal and nonreciprocal algebraic numbers is also investigated. In particular, all cubic units in this set are described and it is shown that the smallest Pisot number is not the measure of a reciprocal number.
over ℚ This is used to show that some numbers considered earlier by Boyd are not Mahler measures. The set of numbers which occur as Mahler measures of both reciprocal and nonreciprocal algebraic numbers is also investigated. In particular, all cubic units in this set are described and it is shown that the smallest Pisot number is not the measure of a reciprocal number.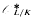 be the subgroup of the unit group
be the subgroup of the unit group 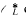 consisting of the elements that are roots of units of
consisting of the elements that are roots of units of 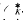 . Denote by
. Denote by 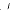 (
(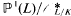 with relative height in the sense of Bergé-Martinet at most
with relative height in the sense of Bergé-Martinet at most 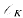 , the ring of integers of
, the ring of integers of 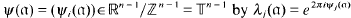 . Then the small region of
. Then the small region of 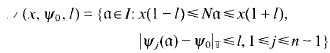
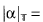 β. where β is the unique real satisyfing
β. where β is the unique real satisyfing 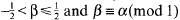 .
.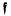 a fixed integral ideal and
a fixed integral ideal and 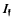 the group of fractional ideals of
the group of fractional ideals of 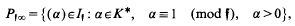
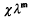 be an arbitrary Groessencharaktere mod f as defined in [15]. Then
be an arbitrary Groessencharaktere mod f as defined in [15]. Then 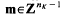 and, for
and, for 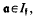
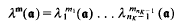
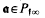 depends only on the
depends only on the 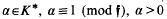 that exists such that
that exists such that 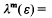 1 for all units ε in
1 for all units ε in 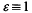 (mod
(mod 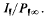
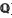 ] =
] = 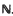 . Most of what we shall discuss is trivial when
. Most of what we shall discuss is trivial when 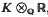 , and is to be regarded as a topological
, and is to be regarded as a topological 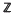 -algebra, dim
-algebra, dim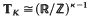 -submodule of rank
-submodule of rank 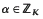 which have a fixed norm
which have a fixed norm 