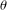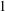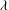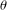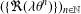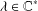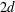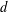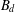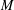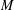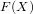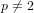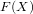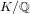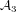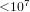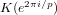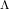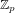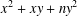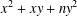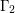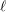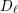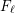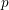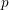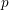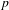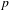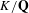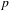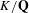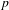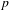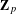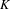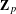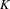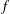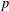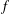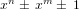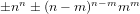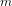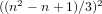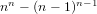Refine listing
Actions for selected content:
364 results in 11Rxx
Some applications of eta-quotients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 565-578
- Print publication:
- June 2016
-
- Article
- Export citation
ON REAL PARTS OF POWERS OF COMPLEX PISOT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 245-253
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
ALGORITHMS FOR GALOIS EXTENSIONS OF GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 513-515
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
ON NUMBER FIELDS WITHOUT A UNIT PRIMITIVE ELEMENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 420-432
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
UNIVERSAL QUADRATIC FORMS AND ELEMENTS OF SMALL NORM IN REAL QUADRATIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 7-14
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
TOPICS IN DIVISIBILITY: PAIRWISE COPRIMALITY, THE GCD OF SHIFTED SETS AND POLYNOMIAL IRREDUCIBILITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 02 January 2016, pp. 167-168
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
THE PROPORTION OF FAILURES OF THE HASSE NORM PRINCIPLE
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 337-347
- Print publication:
- 2016
-
- Article
- Export citation
On
 ${\it\lambda}$ -invariants attached to cyclic cubic number fields
${\it\lambda}$ -invariants attached to cyclic cubic number fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 684-698
-
- Article
-
- You have access
- Export citation
Good families of Drinfeld modular curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 699-712
-
- Article
-
- You have access
- Export citation
REPRESENTATIONS OF INTEGERS BY THE BINARY QUADRATIC FORM
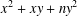 $x^{2}+xy+ny^{2}$
$x^{2}+xy+ny^{2}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 17 November 2015, pp. 182-191
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
ON THE MERTENS–CESÀRO THEOREM FOR NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 199-210
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
ELEMENTS OF ORDER FOUR IN THE NARROW CLASS GROUP OF REAL QUADRATIC FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 28 September 2015, pp. 21-32
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
The Chowla–Selberg formula for abelian CM fields and Faltings heights
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 24 September 2015, pp. 445-476
- Print publication:
- March 2016
-
- Article
- Export citation
Identities for field extensions generalizing the Ohno–Nakagawa relations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 30 June 2015, pp. 2059-2075
- Print publication:
- November 2015
-
- Article
- Export citation
Growth of
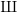 $\unicode[STIX]{x0428}$ in towers for isogenous curves
$\unicode[STIX]{x0428}$ in towers for isogenous curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 30 June 2015, pp. 1981-2005
- Print publication:
- November 2015
-
- Article
- Export citation
Hecke characters associated to Drinfeld modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 2006-2058
- Print publication:
- November 2015
-
- Article
- Export citation
ON THE NON-TRIVIALITY OF THE
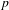 $p$ -ADIC ABEL–JACOBI IMAGE OF GENERALISED HEEGNER CYCLES MODULO
$p$ -ADIC ABEL–JACOBI IMAGE OF GENERALISED HEEGNER CYCLES MODULO 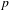 $p$ , II: SHIMURA CURVES
$p$ , II: SHIMURA CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 07 May 2015, pp. 189-222
- Print publication:
- February 2017
-
- Article
- Export citation
INFINITE PRODUCTS OF CYCLOTOMIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 400-411
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
GAPS IN TAYLOR SERIES OF ALGEBRAIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 412-418
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Squarefree values of trinomial discriminants
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 January 2015, pp. 148-169
-
- Article
-
- You have access
- Export citation