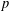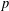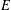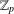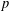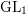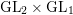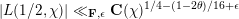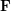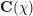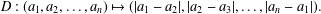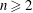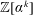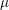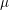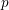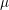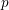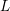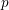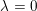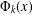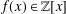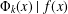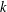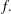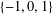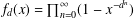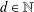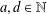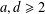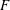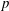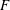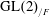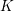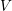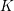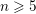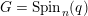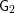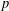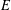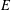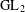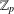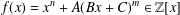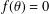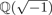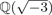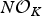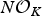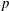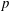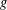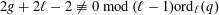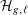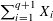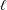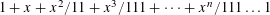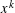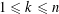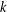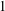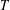Refine listing
Actions for selected content:
364 results in 11Rxx
ON THE EULER CHARACTERISTICS OF SIGNED SELMER GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 09 July 2019, pp. 238-246
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Burgess-like subconvexity for
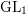 $\text{GL}_{1}$
$\text{GL}_{1}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 04 July 2019, pp. 1457-1499
- Print publication:
- August 2019
-
- Article
- Export citation
PERIODS OF DUCCI SEQUENCES AND ODD SOLUTIONS TO A PELLIAN EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 03 July 2019, pp. 201-205
- Print publication:
- October 2019
-
- Article
-
- You have access
- Open access
- Export citation
On the Discriminants of the Powers of an Algebraic Integer
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 22 May 2019, pp. 481-483
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
CLASS NUMBER FORMULA FOR DIHEDRAL EXTENSIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 21 May 2019, pp. 323-353
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
Congruences with Eisenstein series and
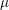 $\unicode[STIX]{x1D707}$-invariants
$\unicode[STIX]{x1D707}$-invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 10 April 2019, pp. 863-901
- Print publication:
- May 2019
-
- Article
- Export citation
CYCLOTOMIC FACTORS OF BORWEIN POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 28 March 2019, pp. 41-47
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
ON GENERALIZED THUE–MORSE FUNCTIONS AND THEIR VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 11 March 2019, pp. 177-201
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Ramification of the Eigencurve at Classical RM Points
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 07 March 2019, pp. 57-88
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Spinor groups with good reduction
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 3 / March 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 484-527
- Print publication:
- March 2019
-
- Article
- Export citation
ON THE SELMER GROUP OF A CERTAIN
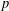 $p$-ADIC LIE EXTENSION
$p$-ADIC LIE EXTENSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 245-255
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
A BRIEF NOTE ON SOME INFINITE FAMILIES OF MONOGENIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 239-244
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
On the Schertz Conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 08 February 2019, pp. 837-845
-
- Article
- Export citation
Binary quadratic forms and ray class groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 695-720
- Print publication:
- April 2020
-
- Article
- Export citation
Annihilators of the Ideal Class Group of a Cyclic Extension of an Imaginary Quadratic Field
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1395-1419
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
ON THE DISTRIBUTION OF THE RATIONAL POINTS ON CYCLIC COVERS IN THE ABSENCE OF ROOTS OF UNITY
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 17 April 2019, pp. 719-742
- Print publication:
- 2019
-
- Article
- Export citation
A CLASS OF IRREDUCIBLE POLYNOMIALS ASSOCIATED WITH PRIME DIVISORS OF VALUES OF CYCLOTOMIC POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1033-1037
- Print publication:
- 2019
-
- Article
- Export citation
ON SIMPLE ZEROS OF THE DEDEKIND ZETA-FUNCTION OF A QUADRATIC NUMBER FIELD
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 22 May 2019, pp. 851-861
- Print publication:
- 2019
-
- Article
- Export citation
A NOTE ON THE EQUIVALENCE OF THE PARITY OF CLASS NUMBERS AND THE SIGNATURE RANKS OF UNITS IN CYCLOTOMIC FIELDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 27 December 2018, pp. 206-214
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
Pólya S3-extensions of ℚ
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1421-1433
- Print publication:
- December 2019
-
- Article
- Export citation