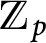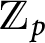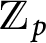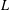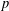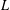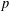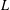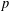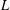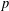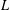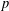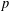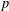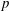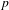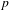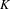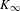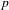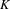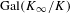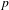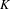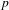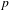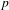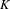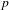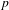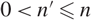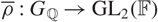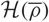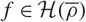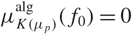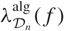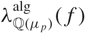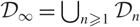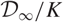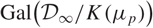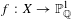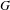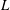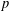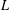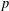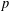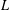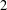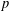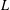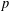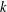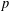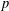Refine listing
Actions for selected content:
364 results in 11Rxx
Bounding the Iwasawa invariants of Selmer groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 1390-1422
- Print publication:
- October 2021
-
- Article
- Export citation
Euler characteristics and their congruences in the positive rank setting
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 228-245
- Print publication:
- March 2021
-
- Article
- Export citation
PERIOD IDENTITIES OF CM FORMS ON QUATERNION ALGEBRAS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 May 2020, e25
-
- Article
-
- You have access
- Open access
- Export citation
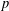 $p$-ADIC
$p$-ADIC 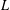 $L$-FUNCTIONS FOR UNITARY GROUPS
$L$-FUNCTIONS FOR UNITARY GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 May 2020, e9
-
- Article
-
- You have access
- Open access
- Export citation
Corrigendum: On the probabilities of local behaviors in abelian field extensions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 15 May 2020, p. 1078
- Print publication:
- May 2020
-
- Article
-
- You have access
- HTML
- Export citation
The Trace Form Over Cyclic Number Fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 14 April 2020, pp. 947-969
- Print publication:
- August 2021
-
- Article
- Export citation
Growth of Fine Selmer Groups in Infinite Towers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 13 March 2020, pp. 921-936
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
WILD RAMIFICATION IN TRINOMIAL EXTENSIONS AND GALOIS GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2020, pp. 106-120
- Print publication:
- January 2021
-
- Article
- Export citation
Lower bound for the Perron–Frobenius degrees of Perron numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 14 January 2020, pp. 1264-1280
- Print publication:
- April 2021
-
- Article
- Export citation
HEURISTICS FOR
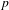 $p$-CLASS TOWERS OF REAL QUADRATIC FIELDS
$p$-CLASS TOWERS OF REAL QUADRATIC FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 26 December 2019, pp. 1429-1452
- Print publication:
- July 2021
-
- Article
- Export citation
On square-free values of large polynomials over the rational function field
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 247-263
- Print publication:
- March 2021
-
- Article
- Export citation
Linear Independence of Logarithms of Cyclotomic Numbers and a Conjecture of Livingston
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 12 December 2019, pp. 31-45
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Variation of the algebraic λ-invariant over a solvable extension
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 21 November 2019, pp. 499-521
- Print publication:
- May 2021
-
- Article
- Export citation
Moments of the Dedekind zeta function and other non-primitive L-functions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 November 2019, pp. 191-219
- Print publication:
- January 2021
-
- Article
- Export citation
Vinogradov’s three primes theorem with primes having given primitive roots
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 05 November 2019, pp. 75-110
- Print publication:
- January 2021
-
- Article
- Export citation
DENSITY RESULTS FOR SPECIALIZATION SETS OF GALOIS COVERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 25 October 2019, pp. 1455-1496
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
One-Level Density of Low-lying Zeros of Quadratic and Quartic Hecke
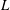 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 30 August 2019, pp. 427-454
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
CODIMENSION TWO CYCLES IN IWASAWA THEORY AND ELLIPTIC CURVES WITH SUPERSINGULAR REDUCTION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 August 2019, e25
-
- Article
-
- You have access
- Open access
- Export citation
SATO–TATE EQUIDISTRIBUTION OF CERTAIN FAMILIES OF ARTIN
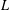 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 August 2019, e23
-
- Article
-
- You have access
- Open access
- Export citation
APPLICATIONS OF LERCH’S THEOREM TO PERMUTATIONS OF QUADRATIC RESIDUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 10 July 2019, pp. 362-371
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation