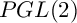 $PGL(2)$ EXTENSION
$PGL(2)$ EXTENSION
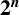 $\boldsymbol {2^n}$
$\boldsymbol {2^n}$
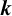 $\boldsymbol {k}$TH POWER RESIDUES
$\boldsymbol {k}$TH POWER RESIDUES
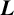 $\boldsymbol {L}$-VALUES
$\boldsymbol {L}$-VALUES
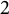 $2$-towers
$2$-towers
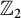 $\mathbb Z_2$-extensions of real quadratic fields
$\mathbb Z_2$-extensions of real quadratic fields