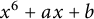 $x^6+ax+b$
$x^6+ax+b$
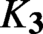 ${K}_{\textbf {3}}$ for imaginary quadratic fields
${K}_{\textbf {3}}$ for imaginary quadratic fields
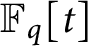 $\mathbb {F}_q[t]$ at negative integers
$\mathbb {F}_q[t]$ at negative integers
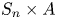 $S_n\times A$ for
$S_n\times A$ for 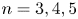 $n = 3,4,5$
$n = 3,4,5$
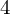 $4$-RANK OF CLASS GROUPS OF DIRICHLET BIQUADRATIC FIELDS
$4$-RANK OF CLASS GROUPS OF DIRICHLET BIQUADRATIC FIELDS
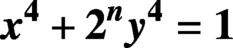 $\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS
$\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS