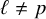 $\ell \neq p$
$\ell \neq p$
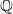 $\mathbb{Q}$
$\mathbb{Q}$
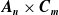 $\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
$\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields