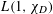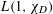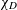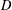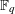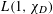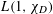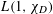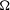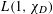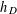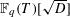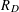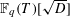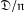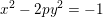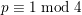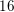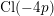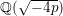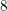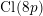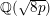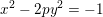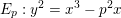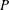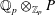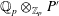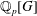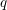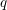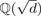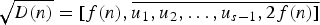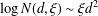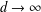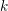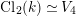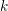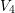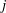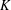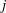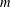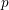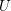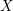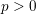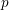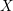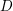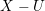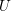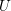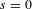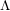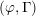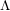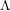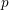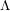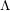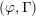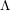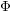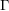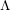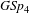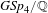Refine listing
Actions for selected content:
364 results in 11Rxx
DUALITY FOR COHOMOLOGY OF CURVES WITH COEFFICIENTS IN ABELIAN VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 42-149
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
COMPLEX MOMENTS AND THE DISTRIBUTION OF VALUES OF
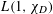 $L(1,\unicode[STIX]{x1D712}_{D})$ OVER FUNCTION FIELDS WITH APPLICATIONS TO CLASS NUMBERS
$L(1,\unicode[STIX]{x1D712}_{D})$ OVER FUNCTION FIELDS WITH APPLICATIONS TO CLASS NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 05 December 2018, pp. 236-271
- Print publication:
- 2019
-
- Article
- Export citation
IDEAL CHAINS IN RESIDUALLY FINITE DEDEKIND DOMAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 56-67
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Spins of prime ideals and the negative Pell equation
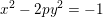 $x^{2}-2py^{2}=-1$
$x^{2}-2py^{2}=-1$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 100-125
- Print publication:
- January 2019
-
- Article
- Export citation
A Generalization of a Theorem of Swan with Applications to Iwasawa Theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 16 November 2018, pp. 656-675
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ON THE GALOIS STRUCTURE OF ARITHMETIC COHOMOLOGY I: COMPACTLY SUPPORTED
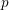 $p$-ADIC COHOMOLOGY
$p$-ADIC COHOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 16 November 2018, pp. 294-321
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
EULER SYSTEMS FOR HILBERT MODULAR SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 15 November 2018, e23
-
- Article
-
- You have access
- Open access
- Export citation
Cyclotomic analogues of finite multiple zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 06 November 2018, pp. 2701-2721
- Print publication:
- December 2018
-
- Article
- Export citation
ON IWASAWA THEORY OF RUBIN–STARK UNITS AND NARROW CLASS GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 673-691
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
HIGHER IDELES AND CLASS FIELD THEORY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 02 October 2018, pp. 214-250
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
Distribution of Class Numbers in Continued Fraction Families of Real Quadratic Fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 20 August 2018, pp. 1193-1212
-
- Article
- Export citation
ALGEBRAIC NUMBERS WITH BOUNDED DEGREE AND WEIL HEIGHT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 212-220
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
DISTRIBUTION OF GALOIS GROUPS OF MAXIMAL UNRAMIFIED 2-EXTENSIONS OVER IMAGINARY QUADRATIC FIELDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 09 July 2018, pp. 166-187
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
THE DENSITY OF
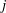 $j$-WISE RELATIVELY
$j$-WISE RELATIVELY  $r$-PRIME ALGEBRAIC INTEGERS
$r$-PRIME ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 06 July 2018, pp. 221-229
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Duality for relative logarithmic de Rham–Witt sheaves and wildly ramified class field theory over finite fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 07 May 2018, pp. 1306-1331
- Print publication:
- June 2018
-
- Article
- Export citation
MAHLER MEASURE OF ‘ALMOST’ RECIPROCAL POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 70-76
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
PERIODS OF DRINFELD MODULES AND LOCAL SHTUKAS WITH COMPLEX MULTIPLICATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 20 March 2018, pp. 175-208
- Print publication:
- January 2020
-
- Article
- Export citation
Irreducibility of polynomials over global fields is diophantine
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 761-772
- Print publication:
- April 2018
-
- Article
- Export citation
The geometry of Hida families II:
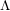 $\unicode[STIX]{x1D6EC}$ -adic
$\unicode[STIX]{x1D6EC}$ -adic 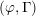 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules and
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules and 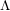 $\unicode[STIX]{x1D6EC}$ -adic Hodge theory
$\unicode[STIX]{x1D6EC}$ -adic Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 719-760
- Print publication:
- April 2018
-
- Article
- Export citation
AN EQUIDISTRIBUTION THEOREM FOR HOLOMORPHIC SIEGEL MODULAR FORMS FOR
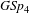 $\mathit{GSp}_{4}$ AND ITS APPLICATIONS
$\mathit{GSp}_{4}$ AND ITS APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 22 February 2018, pp. 351-419
- Print publication:
- March 2020
-
- Article
- Export citation