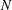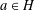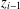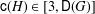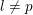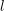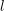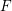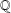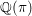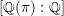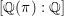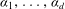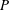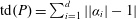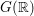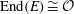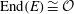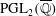Refine listing
Actions for selected content:
364 results in 11Rxx
A database of number fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 December 2014, pp. 595-618
-
- Article
-
- You have access
- Export citation
On the anticyclotomic Iwasawa main conjecture for modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 27 November 2014, pp. 863-897
- Print publication:
- May 2015
-
- Article
- Export citation
THE CATENARY DEGREE OF KRULL MONOIDS II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 21 November 2014, pp. 324-354
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Selmer groups and class groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 416-434
- Print publication:
- March 2015
-
- Article
- Export citation
A classification of all 1-Salem graphs
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 November 2014, pp. 582-594
-
- Article
-
- You have access
- Export citation
Automorphy and irreducibility of some l-adic representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 207-229
- Print publication:
- February 2015
-
- Article
- Export citation
HIGHER ORDER CONGRUENCES AMONGST HASSE–WEIL
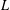 $L$-VALUES
$L$-VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 1-38
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
On fields of rationality for automorphic representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 11 September 2014, pp. 2003-2053
- Print publication:
- December 2014
-
- Article
- Export citation
THE TOTAL DISTANCE FOR TOTALLY POSITIVE ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 391-403
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Refined abelian Stark conjectures and the equivariant leading term conjecture of Burns
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1809-1835
- Print publication:
- November 2014
-
- Article
- Export citation
The real Chevalley involution
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 2127-2142
- Print publication:
- December 2014
-
- Article
- Export citation
SUR LE COMPTAGE DES FIBRÉS DE HITCHIN NILPOTENTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 August 2014, pp. 91-164
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
Class numbers of real cyclotomic fields of composite conductor
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 404-417
-
- Article
-
- You have access
- Export citation
Constructing supersingular elliptic curves with a given endomorphism ring
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 71-91
-
- Article
-
- You have access
- Export citation
Constructing abelian surfaces for cryptography via Rosenhain invariants
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 157-180
-
- Article
-
- You have access
- Export citation
An algorithm for the principal ideal problem in indefinite quaternion algebras
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 366-384
-
- Article
-
- You have access
- Export citation
On the units generated by Weierstrass forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 303-313
-
- Article
-
- You have access
- Export citation
Class number calculation using Siegel functions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 295-302
-
- Article
-
- You have access
- Export citation
Counting imaginary quadratic points via universal torsors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 10 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 1631-1678
- Print publication:
- October 2014
-
- Article
- Export citation
A census of quadratic post-critically finite rational functions defined over
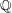 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 July 2014, pp. 314-329
-
- Article
-
- You have access
- Export citation