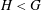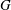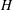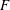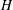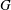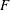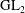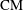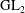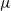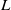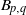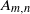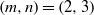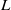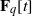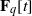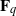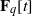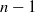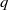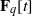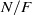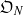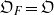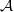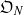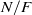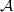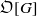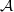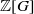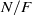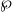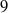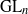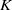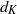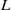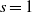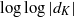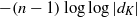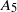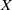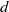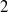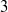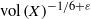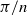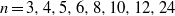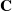Refine listing
Actions for selected content:
364 results in 11Rxx
Modularity of nearly ordinary 2-adic residually dihedral Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 16 June 2014, pp. 1235-1346
- Print publication:
- August 2014
-
- Article
- Export citation
On the beta expansion of Salem numbers of degree 8
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 289-301
-
- Article
-
- You have access
- Export citation
Computation of Galois groups of rational polynomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 141-158
-
- Article
-
- You have access
- Export citation
Galois representations attached to automorphic forms on
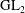 ${\rm GL}_2$ over
${\rm GL}_2$ over 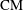 ${\rm CM}$ fields
${\rm CM}$ fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 523-567
- Print publication:
- April 2014
-
- Article
- Export citation
On the
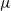 $\mu $ -invariant of the cyclotomic derivative of a Katz p-adic
$\mu $ -invariant of the cyclotomic derivative of a Katz p-adic 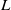 $L$ -function
$L$ -function
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 10 January 2014, pp. 131-148
- Print publication:
- January 2015
-
- Article
- Export citation
LENS SPACE SURGERIES ALONG CERTAIN 2-COMPONENT LINKS RELATED WITH PARK’S RATIONAL BLOW DOWN, AND REIDEMEISTER-TURAEV TORSION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 15 October 2013, pp. 78-126
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Trivial zeros of
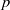 $p$ -adic
$p$ -adic 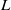 $L$ -functions at near-central points
$L$ -functions at near-central points
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 24 September 2013, pp. 561-598
- Print publication:
- July 2014
-
- Article
- Export citation
REPRESENTING AN ELEMENT IN
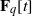 ${\mathbf{F} }_{q} [t] $ AS THE SUM OF TWO IRREDUCIBLES
${\mathbf{F} }_{q} [t] $ AS THE SUM OF TWO IRREDUCIBLES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 23 May 2013, pp. 166-182
- Print publication:
- January 2014
-
- Article
- Export citation
Self-dual integral normal bases and Galois module structure
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 10 May 2013, pp. 1175-1202
- Print publication:
- July 2013
-
- Article
- Export citation
Minimal solvable nonic fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 May 2013, pp. 130-138
-
- Article
-
- You have access
- Export citation
Cusp eigenforms and the hall algebra of an elliptic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 04 March 2013, pp. 914-958
- Print publication:
- June 2013
-
- Article
- Export citation
Logarithmic derivatives of Artin
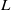 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 568-586
- Print publication:
- April 2013
-
- Article
- Export citation
Hybrid bounds for automorphic forms on ellipsoids over number fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 20 December 2012, pp. 727-758
- Print publication:
- October 2013
-
- Article
- Export citation
Dihedral Iwasawa theory of nearly ordinary quaternionic automorphic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 13 December 2012, pp. 356-416
- Print publication:
- March 2013
-
- Article
- Export citation
RELATIONS IN THE 2-CLASS GROUP OF QUADRATIC NUMBER FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 07 February 2013, pp. 115-120
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Galois groups of chromatic polynomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 281-307
-
- Article
-
- You have access
- Export citation
ORIGAMI RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 02 November 2012, pp. 299-311
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
On Greenberg’s L-invariant of the symmetric sixth power of an ordinary cusp form
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 15 May 2012, pp. 1033-1050
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
A crossed-product approach to the Cuntz–Li algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 429-459
-
- Article
-
- You have access
- Export citation
On the automorphy of l-adic Galois representations with small residual image With an appendix by Robert Guralnick, Florian Herzig, Richard Taylor and Jack Thorne
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 05 April 2012, pp. 855-920
- Print publication:
- October 2012
-
- Article
- Export citation