Refine listing
Actions for selected content:
364 results in 11Rxx
Le lemme fondamental pondéré. I. Constructions géométriques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 6 / November 2010
- Published online by Cambridge University Press:
- 19 May 2010, pp. 1416-1506
- Print publication:
- November 2010
-
- Article
-
- You have access
- Export citation
A lower bound for Garsia’s entropy for certain Bernoulli convolutions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 May 2010, pp. 130-143
-
- Article
-
- You have access
- Export citation
On descent theory and main conjectures in non-commutative Iwasawa theory
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 26 April 2010, pp. 59-118
- Print publication:
- January 2011
-
- Article
- Export citation
On the minimal ramification problem for ℓ-groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 18 March 2010, pp. 599-606
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
On the potential automorphy of certain odd-dimensional Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 10 March 2010, pp. 607-620
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
Special Values of Class Group L-Functions for CM Fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 157-181
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
Conjecture de monodromie-poids pour quelques variétés de Shimura unitaires
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 367-403
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
On the probabilities of local behaviors in abelian field extensions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 08 December 2009, pp. 102-128
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
On quadratic fields generated by the Shanks sequence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 719-729
-
- Article
-
- You have access
- Export citation
The convergence of Euler products over p-adic number fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 583-606
-
- Article
-
- You have access
- Export citation
On Ihara’s lemma for Hilbert modular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 09 September 2009, pp. 1114-1146
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Stark units and the main conjectures for totally real fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 23 October 2009, pp. 1163-1195
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
NONABELIAN NORMAL CM-FIELDS OF DEGREE 2pq
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 01 August 2009, pp. 129-144
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
Subconvexity bounds for automorphic L-functions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 23 July 2009, pp. 95-124
- Print publication:
- January 2010
-
- Article
- Export citation
Geometric Weil representation: local field case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 56-88
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
Integral moments of automorphic L-functions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 16 October 2008, pp. 335-382
- Print publication:
- April 2009
-
- Article
- Export citation
Geometric Waldspurger periods
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 377-438
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Utilisation d’une cohomologie étale équivariante en topologie arithmétique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 32-60
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
On Rubin’s variant of the p-adic Birch and Swinnerton-Dyer conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1374-1398
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
Leading terms of Artin L-functions at s=0 and s=1
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1427-1464
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
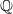 with no more than
with no more than 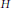
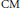
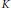


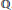
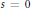

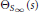
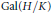
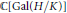
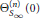
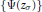
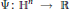
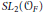
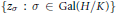
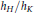
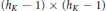
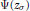
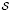 -unit equations as well as bounds for character sums to obtain a lower bound on the number of distinct fields among
-unit equations as well as bounds for character sums to obtain a lower bound on the number of distinct fields among 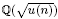 for
for 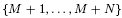 . Fields of this type include the Shanks fields and their generalizations.
. Fields of this type include the Shanks fields and their generalizations.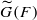 . This is a category of certain perverse sheaves on some stack, on which
. This is a category of certain perverse sheaves on some stack, on which 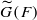 acts by functors. This construction will be used by Lysenko (in [
acts by functors. This construction will be used by Lysenko (in [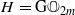 ,
, 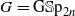 over
over 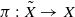 . Let
. Let 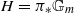 with
with 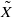 connected. We establish the geometric Langlands functoriality for this pair. Namely, we show that
connected. We establish the geometric Langlands functoriality for this pair. Namely, we show that 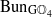 to
to 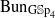 . Based on these calculations, we give three conjectural constructions of certain automorphic sheaves on
. Based on these calculations, we give three conjectural constructions of certain automorphic sheaves on 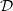 -modules only).
-modules only).