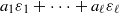Refine listing
Actions for selected content:
364 results in 11Rxx
ROOTS OF UNITY AS QUOTIENTS OF TWO ROOTS OF A POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 10 August 2012, pp. 137-144
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
ON THE EQUATION f(g(x))=f(x)hm(x) FOR COMPOSITE POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 155-161
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
ON TORSION OF CLASS GROUPS OF CM TORI
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 28 March 2012, pp. 305-318
- Print publication:
- July 2012
-
- Article
- Export citation
ON THE DISTRIBUTION OF TORSION POINTS MODULO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 339-347
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
LOG-SINE EVALUATIONS OF MAHLER MEASURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 June 2012, pp. 15-36
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
ON THE CLASS NUMBER AND THE FUNDAMENTAL UNIT OF THE REAL QUADRATIC FIELD

- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 25 January 2012, pp. 359-370
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
From L-series of elliptic curves to Mahler measures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 23 January 2012, pp. 385-414
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Geometric Weil representation in characteristic two
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 13 December 2011, pp. 221-271
- Print publication:
- April 2012
-
- Article
- Export citation
ON THE DISTRIBUTION OF GALOIS GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 21 October 2011, pp. 35-44
- Print publication:
- January 2012
-
- Article
- Export citation
On anticyclotomic μ-invariants of modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 27 July 2011, pp. 1353-1381
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
ON LINEAR COMBINATIONS OF UNITS WITH BOUNDED COEFFICIENTS
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 31 May 2011, pp. 247-262
- Print publication:
- July 2011
-
- Article
- Export citation
On the equivariant Tamagawa number conjecture in tame CM-extensions, II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 04 May 2011, pp. 1179-1204
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
Vanishing of the μ-invariant of p-adic Hecke L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 24 March 2011, pp. 1151-1178
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
Modularity lifting theorems for Galois representations of unitary type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 18 March 2011, pp. 1022-1058
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
Nonsolvable number fields ramified only at 3 and 5
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 15 February 2011, pp. 716-734
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Dichotomy for generic supercuspidal representations of G2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 15 February 2011, pp. 735-783
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Iwasawa theory for modular forms at supersingular primes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 803-838
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
One level density of low-lying zeros of families of L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 07 September 2010, pp. 1-18
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Refined class number formulas and Kolyvagin systems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 17 August 2010, pp. 56-74
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
A non-abelian Stickelberger theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 01 July 2010, pp. 35-55
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
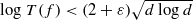 . In the opposite direction, we show that the constant 2cannot be replaced by a number smaller than 1 . These estimates are useful in the study of degenerate and nondegenerate linear recurrence sequences over a number field
. In the opposite direction, we show that the constant 2cannot be replaced by a number smaller than 1 . These estimates are useful in the study of degenerate and nondegenerate linear recurrence sequences over a number field 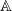 be a commutative algebraic group defined over a number field
be a commutative algebraic group defined over a number field 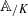 , we determine the average values of
, we determine the average values of 
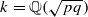 , let
, let 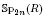 . We also construct a geometric analogue of the Weil representation of Ĝ, this is a triangulated category on which Ĝ acts by functors. This triangulated category and the action are geometric in a suitable sense.
. We also construct a geometric analogue of the Weil representation of Ĝ, this is a triangulated category on which Ĝ acts by functors. This triangulated category and the action are geometric in a suitable sense.