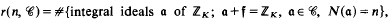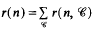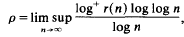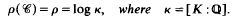Refine listing
Actions for selected content:
364 results in 11Rxx
Uniform distribution and lattice point counting
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 39-50
- Print publication:
- August 1992
-
- Article
-
- You have access
- Export citation
Quartic normal extensions of the rational field
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 3 / December 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 473-482
- Print publication:
- December 1991
-
- Article
-
- You have access
- Export citation
Rigidity of Decomposition laws and number fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-186
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
On the number of integral ideals of given norm and ray-class
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-190
- Print publication:
- June 1991
-
- Article
- Export citation