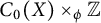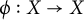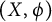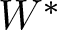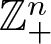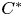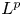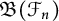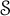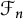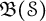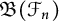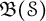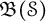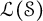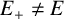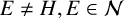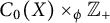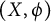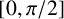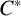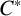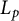Refine listing
Actions for selected content:
81 results in 47Lxx
Ideal structure of uniform Roe algebras: beyond Property A
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simplicity of crossed products by FC-hypercentral groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 28 October 2025, pp. 2272-2319
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KMS states on uniform Roe algebras
- Part of
-
- Journal:
- Canadian Mathematical Communications / Volume 1 / 2025
- Published online by Cambridge University Press:
- 15 August 2025, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
X-ROKHLIN PROPERTY FOR ACTIONS OF COUNTABLE DISCRETE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-11
-
- Article
- Export citation
On Fock covariance for product systems and the reduced Hao–Ng isomorphism problem by discrete actions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1-53
-
- Article
- Export citation
The lattice of C
 $^*$-covers of an operator algebra
$^*$-covers of an operator algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
$C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 366-379
- Print publication:
- October 2025
-
- Article
- Export citation
Compact elements and the hypocompact radical of crossed products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 349-358
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Crossed products as compact quantum metric spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 December 2024, pp. 1-31
-
- Article
- Export citation
Isometric dilations for representations of product systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topologically free actions and ideals in twisted Banach algebra crossed products
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-31
-
- Article
- Export citation
Thompson’s semigroup and the first Hochschild cohomology
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 842-862
- Print publication:
- June 2025
-
- Article
- Export citation
2-LOCAL ISOMETRIES OF SOME NEST ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 367-376
- Print publication:
- October 2024
-
- Article
- Export citation
Tensor algebras of subproduct systems and noncommutative function theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 1587-1608
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ideals with approximate unit in semicrossed products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 12 September 2023, pp. 257-264
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON POSSIBLE VALUES OF THE INTERIOR ANGLE BETWEEN INTERMEDIATE SUBALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 44-66
- Print publication:
- August 2024
-
- Article
- Export citation
TROTTER–KATO PRODUCT FORMULA AND AN APPROXIMATION FORMULA FOR A PROPAGATOR IN SYMMETRIC OPERATOR IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 173-174
- Print publication:
- August 2023
-
- Article
-
- You have access
- HTML
- Export citation
A note on the column–row property
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1244-1254
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CRITERION FOR HYPERSYMMETRY ON DISCRETE GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 05 December 2022, pp. 320-330
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Double relative commutants in coronas of separable C*-algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 345-355
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation