Refine listing
Actions for selected content:
81 results in 47Lxx
APPROXIMATIONS OF SUBHOMOGENEOUS ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 328-337
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
On quotient modules of H2(𝔻n): essential normality and boundary representations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 31 January 2019, pp. 1339-1359
- Print publication:
- June 2020
-
- Article
- Export citation
Fourier Spaces and Completely Isometric Representations of Arens Product Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 717-747
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
INVERSION OF OPERATOR PENCILS ON HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 145-176
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
CONCERNING SUMMABLE SZLENK INDEX
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 59-73
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
SOME RESULTS OF THE
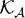 $\mathcal K_{\mathcal A}$-APPROXIMATION PROPERTY FOR BANACH SPACES
$\mathcal K_{\mathcal A}$-APPROXIMATION PROPERTY FOR BANACH SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 09 August 2018, pp. 545-555
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
A New Class of Maximal Triangular Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 909-931
-
- Article
- Export citation
Maximal Ideals in Some Spaces of Bounded Linear Operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 01 February 2018, pp. 251-264
-
- Article
- Export citation
ON THE ORDER STRUCTURE OF REPRESENTABLE FUNCTIONALS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 289-305
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
EMBEDDINGS AND
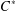 $C^{\ast }$ -ENVELOPES OF EXACT OPERATOR SYSTEMS
$C^{\ast }$ -ENVELOPES OF EXACT OPERATOR SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 274-285
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
NONCLASSICAL SPECTRAL ASYMPTOTICS AND DIXMIER TRACES: FROM CIRCLES TO CONTACT MANIFOLDS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 23 January 2017, e3
-
- Article
-
- You have access
- Open access
- Export citation
BIRKHOFF ORTHOGONALITY IN CLASSICAL
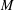 $M$ -IDEALS
$M$ -IDEALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 08 November 2016, pp. 279-288
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Factoriality and Type Classification of k-Graph von Neumann Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 499-518
-
- Article
- Export citation
A SPECTRAL CHARACTERIZATION OF
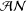 ${\mathcal{A}}{\mathcal{N}}$ OPERATORS
${\mathcal{A}}{\mathcal{N}}$ OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 08 July 2016, pp. 369-391
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
COMPACT ELEMENTS AND OPERATORS OF QUANTUM GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 445-462
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
THE NON-COMMUTATIVE SCHWARTZ SPACE IS WEAKLY AMENABLE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 437-443
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
OPERATOR SYSTEM NUCLEARITY VIA
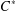 $C^{\ast }$ -ENVELOPES
$C^{\ast }$ -ENVELOPES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 11 May 2016, pp. 356-375
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
MORE ON THE ARENS REGULARITY OF
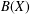 $B(X)$
$B(X)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 296-303
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
SECOND-ORDER NONCOMMUTATIVE DIFFERENTIAL AND LIPSCHITZ STRUCTURES DEFINED BY A CLOSED SYMMETRIC OPERATOR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 25 November 2015, pp. 145-162
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Bilattices and Morita Equivalence of MASA Bimodules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 605-621
-
- Article
- Export citation

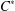



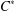
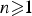
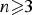

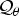
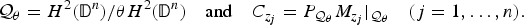
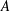
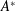

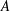
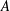
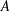
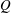
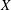
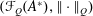
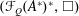
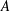

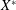
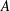
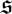
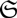
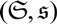
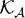
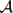
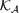
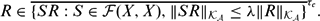
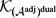
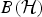
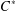
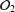
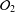
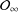
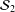
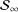
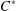
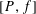
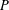
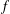
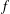
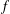
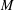
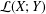
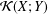
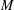
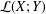
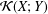
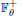 be a single vertex
be a single vertex 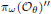 be the von Neumann algebra induced from the Gelfand–Naimark–Segal (GNS) representation of a distinguished state
be the von Neumann algebra induced from the Gelfand–Naimark–Segal (GNS) representation of a distinguished state 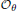 . In this paper we prove the factoriality of
. In this paper we prove the factoriality of 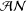
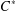
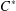
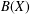
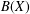
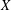
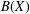
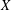

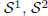 are bilattices that correspond to reflexive MASA bimodules
are bilattices that correspond to reflexive MASA bimodules 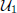 ,
, 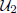 and
and  is an onto bilattice homomorphism, then
is an onto bilattice homomorphism, then