Refine listing
Actions for selected content:
81 results in 47Lxx
THE NON-COMMUTATIVE KHINTCHINE INEQUALITIES FOR
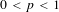 $0<p<1$
$0<p<1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 14 October 2015, pp. 1103-1123
- Print publication:
- November 2017
-
- Article
- Export citation
STABLE PROPERTIES OF HYPERRELEXIVITY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 205-218
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
PERIODIC
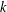 $k$-GRAPH ALGEBRAS REVISITED
$k$-GRAPH ALGEBRAS REVISITED
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 20 April 2015, pp. 267-286
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Some Weighted Group Algebras are Operator Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 05 January 2015, pp. 499-519
-
- Article
-
- You have access
- Export citation
THE
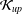 ${\mathcal{K}}_{\mathit{up}}$ -APPROXIMATION PROPERTY AND ITS DUALITY
${\mathcal{K}}_{\mathit{up}}$ -APPROXIMATION PROPERTY AND ITS DUALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 20 November 2014, pp. 364-374
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
A NONSEPARABLE AMENABLE OPERATOR ALGEBRA WHICH IS NOT ISOMORPHIC TO A
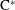 $C^*$ -ALGEBRA
$C^*$ -ALGEBRA
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 March 2014, e2
-
- Article
-
- You have access
- Open access
- Export citation
ON SMALL SUBSPACE LATTICES IN HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 15 October 2013, pp. 44-60
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Operator algebras from the discrete Heisenberg semigroup
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 08 November 2011, pp. 1-22
-
- Article
-
- You have access
- Export citation
IDEALS IN OPERATOR SPACE PROJECTIVE TENSOR PRODUCT OF C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 18 November 2011, pp. 275-288
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
Corrigendum: C*-envelopes of tensor algebras for multivariable dynamics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 20 May 2011, pp. 643-644
-
- Article
-
- You have access
- Export citation
THE GELFAND SPECTRUM OF A NONCOMMUTATIVE C*-ALGEBRA: A TOPOS-THEORETIC APPROACH
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 08 April 2011, pp. 39-52
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
CO-REPRESENTATIONS OF HOPF–VON NEUMANN ALGEBRAS ON OPERATOR SPACES OTHER THAN COLUMN HILBERT SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 205-210
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
C*-envelopes of tensor algebras for multivariable dynamics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 333-351
-
- Article
-
- You have access
- Export citation
AUTOMORPHISMS OF NONSELFADJOINT DIRECTED GRAPH OPERATOR ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 09 October 2009, pp. 175-196
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
Amenability of ultrapowers of Banach algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 307-338
-
- Article
-
- You have access
- Export citation
p-VARIATION OF VECTOR MEASURES WITH RESPECT TO BILINEAR MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 411-430
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
A Class of Limit Algebras Associated with Directed Graphs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-368
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
The strong closure of Boolean algebras of projections in Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-370
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
You can see the arrows in a quiver operator algebra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 111-122
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation
Ideals of compact operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 91-110
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation
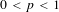
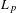
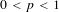
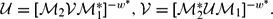
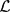
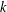
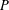
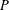
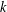
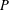
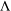
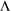
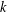
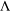
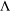
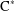
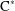
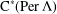
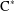
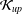
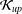
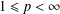
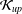
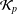
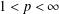
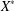
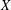
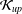
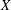
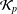
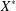
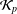
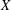
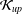
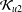
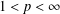
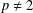
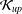
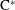
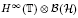 .
.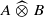 . As an application, a characterization of the prime ideals in the Banach *-algebra
. As an application, a characterization of the prime ideals in the Banach *-algebra 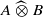 is obtained. In addition, we study the primitive ideals, modular ideals and the maximal modular ideals of
is obtained. In addition, we study the primitive ideals, modular ideals and the maximal modular ideals of 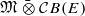 is a Banach algebra if and only if 𝔐 is subhomogeneous or
is a Banach algebra if and only if 𝔐 is subhomogeneous or  is Arens regular, and give some evidence that this is so if and only if
is Arens regular, and give some evidence that this is so if and only if  (
(