Refine listing
Actions for selected content:
80 results in 06Axx
NON-POINTED EXACTNESS, RADICALS, CLOSURE OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 348-361
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
SIMPLE EXTENSIONS OF COMBINATORIAL STRUCTURES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 21 December 2010, pp. 193-214
- Print publication:
- July 2011
-
- Article
- Export citation
ON THE PARTITION MONOID AND SOME RELATED SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 06 December 2010, pp. 273-288
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
PARTIAL ORDERS ON PARTIAL BAER–LEVI SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 195-207
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
PERMUTATION CLASSES OF EVERY GROWTH RATE ABOVE 2.48188
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 182-192
- Print publication:
- January 2010
-
- Article
- Export citation
Special involutions and bulky parabolic subgroups in finite Coxeter groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 141-147
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
Minimum sized fibres in distributive lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 337-350
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
Posets and differential graded algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-19
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
The higher Stasheff-Tamari posets
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-154
- Print publication:
- June 1996
-
- Article
- Export citation
Random high-dimensional orders
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 161-184
- Print publication:
- March 1995
-
- Article
- Export citation
The associated order of a preorder
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-24
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
Biordered sets are biordered subsets of idempotents of semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-268
- Print publication:
- October 1984
-
- Article
-
- You have access
- Export citation
Mildly distributive semilattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-315
- Print publication:
- June 1984
-
- Article
-
- You have access
- Export citation
On the order-theoretical foundation of a theory of quasicompactly generated spaces without separation axiom
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 2 / April 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 194-212
- Print publication:
- April 1984
-
- Article
-
- You have access
- Export citation
Real order-automorphism groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 3 / October 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-261
- Print publication:
- October 1981
-
- Article
-
- You have access
- Export citation
Slim trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 201-214
- Print publication:
- December 1980
-
- Article
-
- You have access
- Export citation
Semilattices with a transitive automorphism group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 1 / February 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 29-34
- Print publication:
- February 1980
-
- Article
-
- You have access
- Export citation
Uniform labelled semilattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-397
- Print publication:
- December 1979
-
- Article
-
- You have access
- Export citation
Extensions of strict partial orders in N-Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 25 / Issue 2 / March 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 241-249
- Print publication:
- March 1978
-
- Article
-
- You have access
- Export citation
Rigidity in order-types
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 24 / Issue 2 / September 1977
- Published online by Cambridge University Press:
- 09 April 2009, pp. 203-215
- Print publication:
- September 1977
-
- Article
-
- You have access
- Export citation
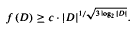 In the process we show that minimum fibre size is a monotone property for a certain class of distributive lattices. This fact depends upon being able to split every maximal antichain of this class of distributive lattices into two parts so that the lattice is the union of the upset of one part and the downset of the other.
In the process we show that minimum fibre size is a monotone property for a certain class of distributive lattices. This fact depends upon being able to split every maximal antichain of this class of distributive lattices into two parts so that the lattice is the union of the upset of one part and the downset of the other.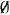 ) corresponding to the empty poset is always contained in
) corresponding to the empty poset is always contained in 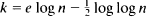 is a threshold function for the appearance of an element of degree
is a threshold function for the appearance of an element of degree 