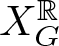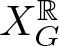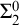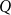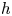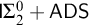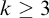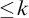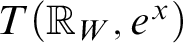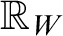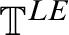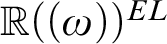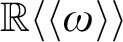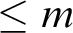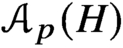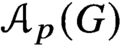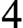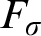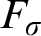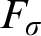Refine listing
Actions for selected content:
80 results in 06Axx
Cohomology of a real toric variety and shellability of posets arising from a graph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 03 November 2023, pp. 1044-1084
-
- Article
- Export citation
WEAK WELL ORDERS AND FRAÏSSÉ’S CONJECTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 September 2023, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CORRECTION TO ‘ON THE COMPLEMENT OF THE ZERO-DIVISOR GRAPH OF A PARTIALLY ORDERED SET’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 170-173
- Print publication:
- February 2024
-
- Article
- Export citation
A NOTE ON BRØNDSTED’S FIXED POINT THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 31 August 2023, pp. 161-166
- Print publication:
- August 2024
-
- Article
- Export citation
Poset Ramsey numbers: large Boolean lattice versus a fixed poset
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 638-653
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Morse theory of Bestvina–Brady type for posets and matchings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 209-220
- Print publication:
- February 2024
-
- Article
- Export citation
(EXTRA)ORDINARY EQUIVALENCES WITH THE ASCENDING/DESCENDING SEQUENCE PRINCIPLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 29 December 2022, pp. 262-307
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLYHEDRAL COMPLETENESS OF INTERMEDIATE LOGICS: THE NERVE CRITERION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 14 November 2022, pp. 342-382
- Print publication:
- March 2024
-
- Article
- Export citation
ORDER TYPES OF MODELS OF FRAGMENTS OF PEANO ARITHMETIC
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 27 April 2022, pp. 182-206
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proper Lie automorphisms of incidence algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 07 February 2022, pp. 702-715
- Print publication:
- September 2022
-
- Article
- Export citation
A DEDEKIND-STYLE AXIOMATIZATION AND THE CORRESPONDING UNIVERSAL PROPERTY OF AN ORDINAL NUMBER SYSTEM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 1396-1418
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MAXIMAL SUBGROUPS OF IDEMPOTENT-GENERATED SEMIGROUPS ASSOCIATED WITH BIORDERED SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 05 January 2022, pp. 341-343
- Print publication:
- April 2022
-
- Article
-
- You have access
- HTML
- Export citation
SURREAL ORDERED EXPONENTIAL FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 1066-1115
- Print publication:
- September 2021
-
- Article
- Export citation
VAUGHT’S CONJECTURE FOR ALMOST CHAINABLE THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 991-1005
- Print publication:
- September 2021
-
- Article
- Export citation
Trees of tangles in infinite separation systems
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 22 July 2021, pp. 297-327
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APPROXIMATING TREES AS COLOURED LINEAR ORDERS AND COMPLETE AXIOMATISATIONS OF SOME CLASSES OF TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 June 2021, pp. 1035-1065
- Print publication:
- September 2021
-
- Article
- Export citation
An approach to Quillen’s conjecture via centralisers of simple groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e48
-
- Article
-
- You have access
- Open access
- Export citation
ON WEAKLY PERFECT ANNIHILATING-IDEAL GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 11 May 2021, pp. 362-372
- Print publication:
- December 2021
-
- Article
- Export citation
TUKEY ORDER AMONG
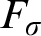 $F_{\sigma }$ IDEALS
$F_{\sigma }$ IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 06 May 2021, pp. 855-870
- Print publication:
- June 2021
-
- Article
- Export citation
COMBINATORICS OF ULTRAFILTERS ON COHEN AND RANDOM ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 109-126
- Print publication:
- March 2022
-
- Article
- Export citation