Refine listing
Actions for selected content:
363 results in 35Qxx
A CONTINUOUS INTERPOLATION BETWEEN CONSERVATIVE AND DISSIPATIVE SOLUTIONS FOR THE TWO-COMPONENT CAMASSA–HOLM SYSTEM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 07 January 2015, e1
-
- Article
-
- You have access
- Open access
- Export citation
DYNAMIC MULTI-STRUCTURE IN MODELLING A TRANSITION FLEXURAL WAVE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 444-456
- Print publication:
- May 2015
-
- Article
- Export citation
PROPAGATION OF SEMICLASSICAL WAVE PACKETS THROUGH AVOIDED EIGENVALUE CROSSINGS IN NONLINEAR SCHRÖDINGER EQUATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 20 October 2014, pp. 319-365
- Print publication:
- April 2016
-
- Article
- Export citation
GLOBAL WELL-POSEDNESS AND INSTABILITY OF A NONLINEAR SCHRÖDINGER EQUATION WITH HARMONIC POTENTIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 78-103
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Multi-solitons for nonlinear Klein–Gordon equations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 09 June 2014, e15
-
- Article
-
- You have access
- Open access
- Export citation
CARLEMAN ESTIMATE AND UNIQUE CONTINUATION PROPERTY FOR THE LINEAR STOCHASTIC KORTEWEG–DE VRIES EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 283-294
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
VORTEX LIQUIDS AND THE GINZBURG–LANDAU EQUATION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 27 May 2014, e11
-
- Article
-
- You have access
- Open access
- Export citation
A NEW UNIQUE CONTINUATION PROPERTY FOR THE KORTEWEG–DE VRIES EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 10 January 2014, pp. 90-98
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Probabilistic Methods for the Incompressible Navier–Stokes Equations With Space Periodic Conditions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 742-772
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
AN IMPROVED SECOND-ORDER NUMERICAL METHOD FOR THE GENERALIZED BURGERS–FISHER EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 3 / January 2013
- Published online by Cambridge University Press:
- 12 June 2013, pp. 181-199
-
- Article
-
- You have access
- Export citation
Compactness properties of critical nonlinearities and nonlinear Schrödinger equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 05 April 2013, pp. 427-441
-
- Article
-
- You have access
- Export citation
MASS CONCENTRATION WITH MIXED NORM FOR A NONELLIPTIC SCHRÖDINGER EQUATION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 07 March 2013, pp. 238-258
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
MODELLING THE ELECTRON WITH COSSERAT ELASTICITY
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 349-370
- Print publication:
- July 2012
-
- Article
- Export citation
A result of multiplicity of solutions for a class of quasilinear equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 291-309
-
- Article
-
- You have access
- Export citation
GLOBAL WELL-POSEDNESS FOR THE GENERALISED FOURTH-ORDER SCHRÖDINGER EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 07 February 2012, pp. 371-379
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
NEW EXACT SOLUTIONS OF COUPLED (2+1)-DIMENSIONAL NONLINEAR SYSTEMS OF SCHRÖDINGER EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 1 / July 2010
- Published online by Cambridge University Press:
- 03 May 2011, pp. 110-121
-
- Article
-
- You have access
- Export citation
THE INVISCID LIMIT OF THE MODIFIED BENJAMIN–ONO–BURGERS EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 06 December 2010, pp. 301-320
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
BLOW-UP OF SMOOTH SOLUTIONS TO THE NAVIER–STOKES EQUATIONS OF COMPRESSIBLE VISCOUS HEAT-CONDUCTING FLUIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 01 April 2010, pp. 239-246
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
A TWO-LEVEL DEFECT–CORRECTION METHOD FOR NAVIER–STOKES EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 21 October 2009, pp. 442-454
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
A cross-constrained variational problem for the generalized Davey–Stewartson system
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 67-77
-
- Article
-
- You have access
- Export citation


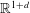
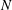
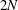
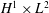
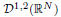 and
and 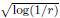 of the respective Hardy-type inequalities, as well as compactness of the limiting Sobolev embeddings once the Sobolev norm is appended by a potential term whose growth at singularities exceeds that of the corresponding Hardy-type potential.
of the respective Hardy-type inequalities, as well as compactness of the limiting Sobolev embeddings once the Sobolev norm is appended by a potential term whose growth at singularities exceeds that of the corresponding Hardy-type potential.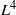
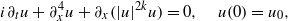
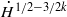 . With small initial data we obtain global well-posedness results. Our proof relies heavily on the method developed by Kenig
. With small initial data we obtain global well-posedness results. Our proof relies heavily on the method developed by Kenig