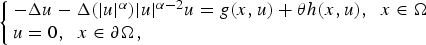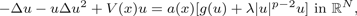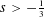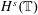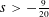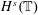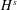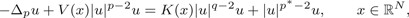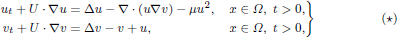Refine listing
Actions for selected content:
363 results in 35Qxx
Perturbed Schrödinger lattice systems: existence of homoclinic solutions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1083-1096
- Print publication:
- August 2019
-
- Article
- Export citation
Uniform moment propagation for the Becker--Döring equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 995-1015
- Print publication:
- August 2019
-
- Article
- Export citation
Finite speed of disturbance for the nonlinear Schrödinger equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1405-1419
- Print publication:
- December 2019
-
- Article
- Export citation
AN IMPROVED RESULT ON GROUND STATE SOLUTIONS OF QUASILINEAR SCHRÖDINGER EQUATIONS WITH SUPER-LINEAR NONLINEARITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 231-241
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Multiple Solutions of Sublinear Quasilinear Schrödinger Equations with Small Perturbations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 471-488
-
- Article
- Export citation
Dynamics and asymptotic profiles of endemic equilibrium for two frequency-dependent SIS epidemic models with cross-diffusion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 26-56
-
- Article
- Export citation
The time-dependent Schrödinger equation with piecewise constant potentials
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 57-83
-
- Article
- Export citation
Targeted energy transfer in stochastically excited system with nonlinear energy sink
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 18 September 2018, pp. 869-886
-
- Article
- Export citation
Asymptotic and transient behaviour for a nonlocal problem arising in population genetics
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 84-110
-
- Article
- Export citation
The Korteweg–de Vries, Burgers and Whitham limits for a spatially periodic Boussinesq model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 191-217
- Print publication:
- February 2019
-
- Article
- Export citation
On the well-posedness and asymptotic behaviour of the generalized Korteweg–de Vries–Burgers equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 219-260
- Print publication:
- February 2019
-
- Article
- Export citation
THE ISOPERIMETRIC QUOTIENT OF A CONVEX BODY DECREASES MONOTONICALLY UNDER THE EIKONAL ABRASION MODEL
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 119-129
- Print publication:
- 2019
-
- Article
- Export citation
Least Energy Nodal Solutions for a Defocusing Schrödinger Equation with Supercritical Exponent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 16 August 2018, pp. 1-23
-
- Article
- Export citation
Long wave approximation for water waves under a Coriolis forcing and the Ostrovsky equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 1201-1237
- Print publication:
- December 2018
-
- Article
- Export citation
RECIPROCITY RELATIONS FOR A CONDUCTIVE SCATTERER WITH A CHIRAL CORE IN QUASI-STATIC FORM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
- Published online by Cambridge University Press:
- 03 July 2018, pp. 86-94
-
- Article
-
- You have access
- Export citation
CONDITIONAL LARGE INITIAL DATA SCATTERING RESULTS FOR THE DIRAC–KLEIN–GORDON SYSTEM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 21 June 2018, e9
-
- Article
-
- You have access
- Open access
- Export citation
Coagulation and universal scaling limits for critical Galton–Watson processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 504-542
- Print publication:
- June 2018
-
- Article
- Export citation
GLOBAL WELL-POSEDNESS OF THE PERIODIC CUBIC FOURTH ORDER NLS IN NEGATIVE SOBOLEV SPACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 11 May 2018, e5
-
- Article
-
- You have access
- Open access
- Export citation
Quasilinear Scalar Field Equations Involving Critical Sobolev Exponents and Potentials Vanishing at Infinity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 30 April 2018, pp. 705-733
-
- Article
- Export citation
Sharp decay estimates in a bioconvection model with quadratic degradation in bounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 25 April 2018, pp. 939-955
- Print publication:
- October 2018
-
- Article
- Export citation