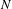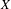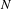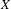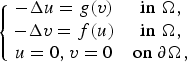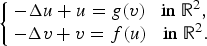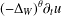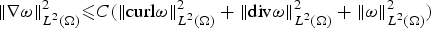Refine listing
Actions for selected content:
363 results in 35Qxx
The massive Thirring system in the quarter plane
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 23 April 2019, pp. 2387-2416
- Print publication:
- October 2020
-
- Article
- Export citation
Local existence of strong solutions and weak–strong uniqueness for the compressible Navier–Stokes system on moving domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 01 April 2019, pp. 2255-2300
- Print publication:
- October 2020
-
- Article
- Export citation
Global well-posedness and large time behaviour of the viscous liquid-gas two-phase flow model in ℝ3
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 14 March 2019, pp. 1999-2024
- Print publication:
- August 2020
-
- Article
- Export citation
Regularity results for the 2D critical Oldroyd-B model in the corotational case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1871-1913
- Print publication:
- August 2020
-
- Article
- Export citation
VARIATIONS OF BPS STRUCTURE AND A LARGE RANK LIMIT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2019, pp. 103-135
- Print publication:
- January 2021
-
- Article
- Export citation
Standing waves of modified Schrödinger equations coupled with the Chern–Simons gauge theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1915-1936
- Print publication:
- August 2020
-
- Article
- Export citation
On a model for phase separation on biological membranes and its relation to the Ohta–Kawasaki equation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 11 March 2019, pp. 297-338
-
- Article
- Export citation
A STUDY ON NUMERICAL MODELLING OF VECTOR-BORNE DISEASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 06 March 2019, pp. 523-524
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
A particle system approach to aggregation phenomena
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 282-306
- Print publication:
- March 2019
-
- Article
- Export citation
Ground state solutions of Hamiltonian elliptic systems in dimension two
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 12 February 2019, pp. 1737-1768
- Print publication:
- August 2020
-
- Article
- Export citation
Ooid growth: Uniqueness of time-invariant, smooth shapes in 2D
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 08 February 2019, pp. 172-182
-
- Article
- Export citation
GLOBAL EXISTENCE OF WEAK SOLUTIONS FOR STRONGLY DAMPED WAVE EQUATIONS WITH NONLINEAR BOUNDARY CONDITIONS AND BALANCED POTENTIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 432-444
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
On critical and supercritical pseudo-relativistic nonlinear Schrödinger equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1241-1263
- Print publication:
- June 2020
-
- Article
- Export citation
A note on a positive solution of a null mass nonlinear field equation in exterior domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 841-870
- Print publication:
- April 2020
-
- Article
- Export citation
Spectral transitions for Aharonov-Bohm Laplacians on conical layers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1663-1687
- Print publication:
- December 2019
-
- Article
- Export citation
Long-time asymptotic expansions for Navier-Stokes equations with power-decaying forces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 22 January 2019, pp. 569-606
- Print publication:
- April 2020
-
- Article
- Export citation
Kolmogorov's dissipation number and the number of degrees of freedom for the 3D Navier–Stokes equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 15 January 2019, pp. 429-446
- Print publication:
- April 2019
-
- Article
- Export citation
Existence of travelling waves with the critical speed for an influenza model with treatment
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 232-245
-
- Article
- Export citation
STOCHASTIC NAVIER–STOKES EQUATIONS ON 2D ROTATING SPHERES WITH STABLE LÉVY NOISE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 344-345
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
On the boundary conditions in estimating ∇ω by div ω and curl ω
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 739-760
- Print publication:
- June 2019
-
- Article
- Export citation