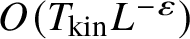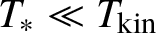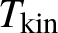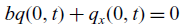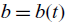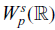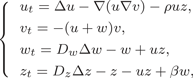Refine listing
Actions for selected content:
363 results in 35Qxx
PRICING TIMER OPTIONS: SECOND-ORDER MULTISCALE STOCHASTIC VOLATILITY ASYMPTOTICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 23 August 2021, pp. 249-267
-
- Article
- Export citation
Positive solutions for a degenerate Kirchhoff problem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 19 August 2021, pp. 675-688
-
- Article
- Export citation
On travelling wave solutions of a model of a liquid film flowing down a fibre
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 12 August 2021, pp. 864-893
-
- Article
- Export citation
OPTIMAL CONTROL OF THE DECUMULATION OF A RETIREMENT PORTFOLIO WITH VARIABLE SPENDING AND DYNAMIC ASSET ALLOCATION
- Part of
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 51 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 28 July 2021, pp. 905-938
- Print publication:
- September 2021
-
- Article
- Export citation
On the derivation of the wave kinetic equation for NLS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 23 July 2021, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invasion fronts and adaptive dynamics in a model for the growth of cell populations with heterogeneous mobility
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 766-783
-
- Article
- Export citation
Direction-dependent turning leads to anisotropic diffusion and persistence
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 23 June 2021, pp. 729-765
-
- Article
- Export citation
Nehari–Pohožaev-type ground state solutions of Kirchhoff-type equation with singular potential and critical exponent
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 21 June 2021, pp. 473-495
- Print publication:
- June 2022
-
- Article
- Export citation
Cahn–Hilliard equations on an evolving surface
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 16 June 2021, pp. 937-1000
-
- Article
- Export citation
Linear evolution equations on the half-line with dynamic boundary conditions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 505-537
-
- Article
- Export citation
Dynamics of an infection age-space structured cholera model with Neumann boundary condition
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 393-422
-
- Article
- Export citation
On regularity properties of a surface growth model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 09 March 2021, pp. 1869-1892
- Print publication:
- December 2021
-
- Article
- Export citation
Local well-posedness for Frémond’s model of complete damage in elastic solids
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 01 March 2021, pp. 309-327
-
- Article
- Export citation
Strong well-posedness and inverse identification problem of a non-local phase field tumour model with degenerate mobilities
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 22 February 2021, pp. 267-308
-
- Article
-
- You have access
- Open access
- Export citation
Well-posedness of the Muskat problem in subcritical Lp-Sobolev spaces
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 224-266
-
- Article
- Export citation
Dispersive fractalisation in linear and nonlinear Fermi–Pasta–Ulam–Tsingou lattices
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 12 January 2021, pp. 820-845
-
- Article
-
- You have access
- Open access
- Export citation
On symmetric wedge mode of an elastic solid
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 11 January 2021, pp. 201-223
-
- Article
- Export citation
VARIATION ON A THEME BY KISELEV AND NAZAROV: HÖLDER ESTIMATES FOR NONLOCAL TRANSPORT-DIFFUSION, ALONG A NON-DIVERGENCE-FREE BMO FIELD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1651-1675
- Print publication:
- September 2022
-
- Article
- Export citation
Asymptotic stability of spatial homogeneity in a haptotaxis model for oncolytic virotherapy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 81-101
- Print publication:
- February 2022
-
- Article
- Export citation
The convergence rate of the fast signal diffusion limit for a Keller–Segel–Stokes system with large initial data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 23 December 2020, pp. 1972-2012
- Print publication:
- December 2021
-
- Article
- Export citation