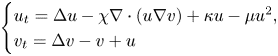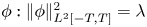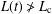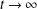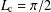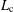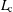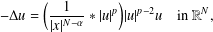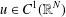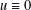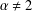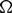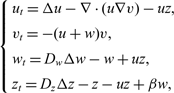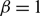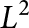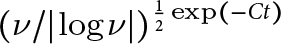Refine listing
Actions for selected content:
363 results in 35Qxx
Regularity criterion on the energy conservation for the compressible Navier–Stokes equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 11 December 2020, pp. 1954-1971
- Print publication:
- December 2021
-
- Article
- Export citation
Steady Euler flows and Beltrami fields in high dimensions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 07 December 2020, pp. 3610-3633
- Print publication:
- December 2021
-
- Article
- Export citation
Comparing the best-reply strategy and mean-field games: The stationary case
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 20 November 2020, pp. 79-110
-
- Article
- Export citation
Solving the 4NLS with white noise initial data
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 18 November 2020, e48
-
- Article
-
- You have access
- Open access
- Export citation
Coarse graining of a Fokker–Planck equation with excluded volume effects preserving the gradient flow structure
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 22 September 2020, pp. 711-745
-
- Article
-
- You have access
- Open access
- Export citation
Global well-posedness and decay estimates of strong solutions to the nonhomogeneous Boussinesq equations for magnetohydrodynamics convection
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 15 September 2020, pp. 1543-1567
- Print publication:
- October 2021
-
- Article
- Export citation
Immediate smoothing and global solutions for initial data in L1 × W1,2 in a Keller–Segel system with logistic terms in 2D
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 02 September 2020, pp. 1204-1224
- Print publication:
- August 2021
-
- Article
- Export citation
A convergence to the Navier–Stokes–Maxwell system with solenoidal Ohm's law from a two-fluid model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 26 August 2020, pp. 1094-1115
- Print publication:
- June 2021
-
- Article
- Export citation
Stability of periodic waves for the fractional KdV and NLS equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 12 August 2020, pp. 1171-1203
- Print publication:
- August 2021
-
- Article
- Export citation
Global dynamics and spatio-temporal patterns of predator–prey systems with density-dependent motion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 12 August 2020, pp. 652-682
-
- Article
- Export citation
Does indirectness of signal production reduce the explosion-supporting potential in chemotaxis–haptotaxis systems? Global classical solvability in a class of models for cancer invasion (and more)
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 17 July 2020, pp. 618-651
-
- Article
- Export citation
GLOBAL SUBELLIPTIC ESTIMATES FOR KRAMERS–FOKKER–PLANCK OPERATORS WITH SOME CLASS OF POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 22 June 2020, pp. 675-711
- Print publication:
- March 2022
-
- Article
- Export citation
CRITICAL LENGTH FOR THE SPREADING–VANISHING DICHOTOMY IN HIGHER DIMENSIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 19 June 2020, pp. 3-17
-
- Article
-
- You have access
- Export citation
STABLE SOLUTIONS TO THE STATIC CHOQUARD EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 10 June 2020, pp. 471-478
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Analysis of a spatially inhomogeneous stochastic partial differential equation epidemic model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 613-636
- Print publication:
- June 2020
-
- Article
- Export citation
Local minimizers in absence of ground states for the critical NLS energy on metric graphs
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 22 May 2020, pp. 705-733
- Print publication:
- April 2021
-
- Article
- Export citation
A LIPSCHITZ METRIC FOR THE CAMASSA–HOLM EQUATION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 21 May 2020, e27
-
- Article
-
- You have access
- Open access
- Export citation
A critical virus production rate for efficiency of oncolytic virotherapy
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 May 2020, pp. 301-316
-
- Article
- Export citation
Edge corrections for parallel-plate capacitors
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 30 April 2020, pp. 226-241
-
- Article
-
- You have access
- Open access
- Export citation
A Note on the Vanishing Viscosity Limit in the Yudovich Class
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 24 April 2020, pp. 112-122
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- Export citation