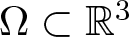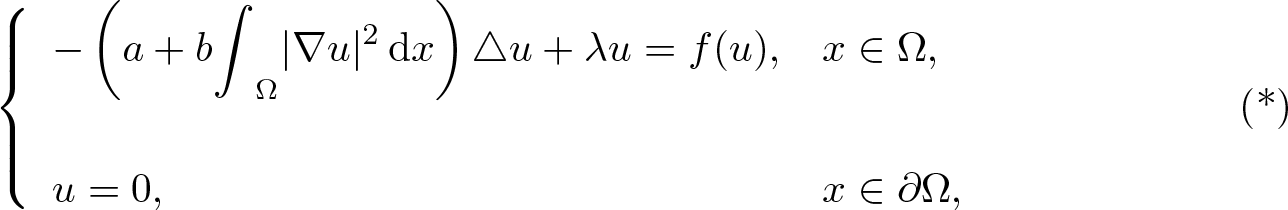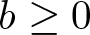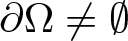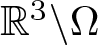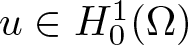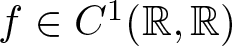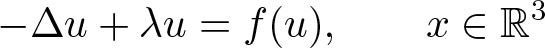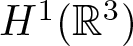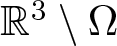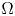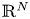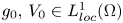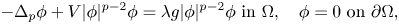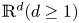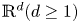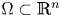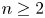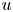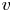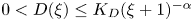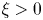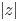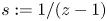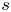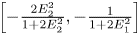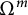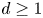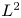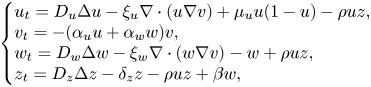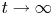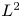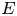Refine listing
Actions for selected content:
363 results in 35Qxx
Existence of positive solutions for Kirchhoff-type problem in exterior domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 04 April 2023, pp. 182-217
-
- Article
- Export citation
Vanishing limit for the three-dimensional incompressible Phan-Thien–Tanner system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 673-698
- Print publication:
- June 2024
-
- Article
- Export citation
Global existence and large time behaviour for the pressureless Euler–Naver–Stokes system in ℝ3
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 22 February 2023, pp. 328-352
- Print publication:
- February 2024
-
- Article
- Export citation
A note on energy equality for the fractional Navier-Stokes equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 February 2023, pp. 201-208
- Print publication:
- February 2024
-
- Article
- Export citation
A modelling framework for efficient reduced order simulations of parametrised lithium-ion battery cells
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 29 November 2022, pp. 554-591
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modelling, simulation and optimisation of parabolic trough power plants
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 11 October 2022, pp. 592-615
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the optimization of the first weighted eigenvalue
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 1777-1804
- Print publication:
- December 2023
-
- Article
- Export citation
Long-time asymptotics of the modified KdV equation in weighted Sobolev spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 23 August 2022, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zero-electron-mass limit of the compressible Navier–Stokes–Poisson equations with well/ill-prepared initial data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 1439-1466
- Print publication:
- October 2023
-
- Article
- Export citation
Quadratic Klein-Gordon equations with a potential in one dimension
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 11 July 2022, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integration of the modified double layer potential of the vector boundary element method for eddy current problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 16 June 2022, pp. 385-407
-
- Article
- Export citation
Finite-time blow-up in a repulsive chemotaxis-consumption system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 1150-1166
- Print publication:
- August 2023
-
- Article
- Export citation
Global Strichartz estimates for the Dirac equation on symmetric spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 May 2022, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral representation of hydraulic permeability
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 May 2022, pp. 907-936
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence of stationary vortex sheets for the 2D incompressible Euler equation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 05 May 2022, pp. 828-853
- Print publication:
- June 2023
-
- Article
- Export citation
Absence of singularities in solutions for the compressible Euler equations with source terms in $\mathbb {R}^d$
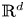
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 26 April 2022, pp. 978-1001
- Print publication:
- June 2023
-
- Article
- Export citation
Stability and exponential decay for magnetohydrodynamic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 853-880
- Print publication:
- June 2023
-
- Article
- Export citation
Steady state diffusion in tubular structures: Assessment of one-dimensional models
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 262-279
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic behaviour in a doubly haptotactic cross-diffusion model for oncolytic virotherapy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 19 April 2022, pp. 881-906
- Print publication:
- June 2023
-
- Article
- Export citation
Exponential decay for the KdV equation on ℝ with new localized dampings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 1073-1098
- Print publication:
- August 2023
-
- Article
- Export citation