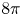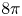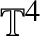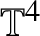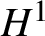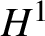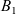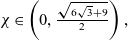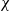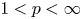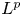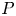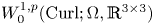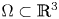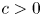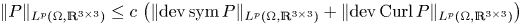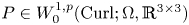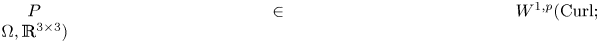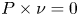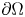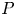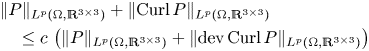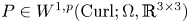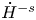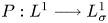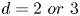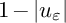Refine listing
Actions for selected content:
363 results in 35Qxx
PATTERN FORMATION IN ELECTRICALLY COUPLED PACEMAKER CELLS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 01 April 2022, pp. 165-166
- Print publication:
- August 2022
-
- Article
-
- You have access
- HTML
- Export citation
The stability analysis of a 2D Keller–Segel–Navier–Stokes system in fast signal diffusion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 31 March 2022, pp. 160-209
-
- Article
-
- You have access
- HTML
- Export citation
Soliton solutions for a class of Schrödinger equations with a positive quasilinear term and critical growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 279-301
-
- Article
- Export citation
Stationary solutions to the Keller–Segel equation on curved planes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 31 January 2022, pp. 327-343
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Resonance-based schemes for dispersive equations via decorated trees
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 January 2022, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unconditional uniqueness for the energy-critical nonlinear Schrödinger equation on
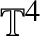 $\mathbb {T}^{4}$
$\mathbb {T}^{4}$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 January 2022, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Macroscopic limit of a kinetic model describing the switch in T cell migration modes via binary interactions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 23 December 2021, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
Decay of weak solutions to Vlasov equation coupled with a shear thickening fluid
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 167-176
- Print publication:
- February 2023
-
- Article
- Export citation
Inverse scattering transforms for non-local reverse-space matrix non-linear Schrödinger equations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 01 December 2021, pp. 1062-1082
-
- Article
-
- You have access
- HTML
- Export citation
On the global existence and qualitative behaviour of one-dimensional solutions to a model for urban crime
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 02 November 2021, pp. 919-959
-
- Article
- Export citation
Charge transport modelling of Lithium-ion batteries
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 21 October 2021, pp. 983-1031
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lp-trace-free generalized Korn inequalities for incompatible tensor fields in three space dimensions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 1477-1508
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global well-posedness and decay estimates for three-dimensional compressible Navier–Stokes–Allen–Cahn systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 1291-1322
- Print publication:
- October 2022
-
- Article
- Export citation
Decay properties for the incompressible Navier-Stokes flows in a half space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 1509-1532
- Print publication:
- December 2022
-
- Article
- Export citation
Well-posedness of the free surface problem on a Newtonian fluid between cylinders rotating at different speeds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 21 September 2021, pp. 1251-1276
- Print publication:
- October 2022
-
- Article
- Export citation
Global regularity criterion for the dissipative systems modelling electrohydrodynamics involving the middle eigenvalue of the strain tensor
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 21 September 2021, pp. 1277-1290
- Print publication:
- October 2022
-
- Article
- Export citation
Global regularity for the micropolar Rayleigh-Bénard problem with only velocity dissipation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 26 August 2021, pp. 1109-1138
- Print publication:
- October 2022
-
- Article
- Export citation
ENERGY CONCENTRATION PROPERTIES OF A p-GINZBURG–LANDAU MODEL
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 25 August 2021, pp. 494-515
- Print publication:
- September 2022
-
- Article
- Export citation
ON THE INSTABILITY OF PERIODIC WAVES FOR DISPERSIVE EQUATIONS—REVISITED
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 25 August 2021, pp. 471-493
- Print publication:
- September 2022
-
- Article
- Export citation
AN ANALYTICAL OPTION PRICING FORMULA FOR MEAN-REVERTING ASSET WITH TIME-DEPENDENT PARAMETER
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 23 August 2021, pp. 178-202
-
- Article
- Export citation