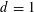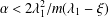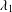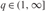Refine listing
Actions for selected content:
363 results in 35Qxx
Uniform convergence in von Neumann’s ergodic theorem in the absence of a spectral gap
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 1601-1611
- Print publication:
- June 2021
-
- Article
- Export citation
ANOMALOUS DIFFUSION PROCESSES: STOCHASTIC MODELS AND THEIR PROPERTIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 27 March 2020, pp. 514-517
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Relaxation of the Cahn–Hilliard equation with singular single-well potential and degenerate mobility
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 24 March 2020, pp. 89-112
-
- Article
- Export citation
A characterization of 3D steady Euler flows using commuting zero-flux homologies
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 18 March 2020, pp. 2166-2181
- Print publication:
- July 2021
-
- Article
-
- You have access
- Open access
- Export citation
LONG TIME BEHAVIOR OF THE SOLUTIONS OF NLW ON THE
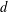 $d$-DIMENSIONAL TORUS
$d$-DIMENSIONAL TORUS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 March 2020, e12
-
- Article
-
- You have access
- Open access
- Export citation
Multiple bound states of higher topological type for semi-classical Choquard equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 04 March 2020, pp. 329-355
- Print publication:
- February 2021
-
- Article
- Export citation
ON A CLASS OF NONLINEAR SCHRÖDINGER EQUATIONS ON FINITE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 477-487
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
A stochastic-statistical residential burglary model with independent Poisson clocks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 05 February 2020, pp. 32-58
-
- Article
-
- You have access
- Open access
- Export citation
Existence, non-existence and blow-up behaviour of minimizers for the mass-critical fractional non-linear Schrödinger equations with periodic potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 13 January 2020, pp. 3252-3292
- Print publication:
- December 2020
-
- Article
- Export citation
THE GLOBAL CAUCHY PROBLEM FOR THE NLS WITH HIGHER ORDER ANISOTROPIC DISPERSION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 45-53
- Print publication:
- January 2021
-
- Article
-
- You have access
- Open access
- Export citation
Steady states and dynamics of a thin-film-type equation with non-conserved mass
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 22 November 2019, pp. 968-1001
-
- Article
- Export citation
About a cavitation model including bubbles in thin film lubrication: A first mathematical analysis
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 14 October 2019, pp. 828-853
-
- Article
- Export citation
Dispersionless integrable hierarchies and GL(2, ℝ) geometry
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 08 October 2019, pp. 129-154
- Print publication:
- January 2021
-
- Article
- Export citation
Mass transport in Fokker–Planck equations with tilted periodic potential
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 30 September 2019, pp. 709-736
-
- Article
- Export citation
Existence of multi-travelling waves in capillary fluids
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 19 August 2019, pp. 2905-2936
- Print publication:
- December 2020
-
- Article
- Export citation
STOCHASTIC NONLINEAR SCHRÖDINGER EQUATION WITH ALMOST SPACE–TIME WHITE NOISE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 21 June 2019, pp. 44-67
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
GLOBAL ATTRACTOR FOR WEAKLY DAMPED, FORCED mKdV EQUATION BELOW ENERGY SPACE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 241 / March 2021
- Published online by Cambridge University Press:
- 20 June 2019, pp. 171-203
- Print publication:
- March 2021
-
- Article
- Export citation
ON STABILITY OF PHYSICALLY REASONABLE SOLUTIONS TO THE TWO-DIMENSIONAL NAVIER–STOKES EQUATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 16 May 2019, pp. 517-568
- Print publication:
- March 2021
-
- Article
- Export citation
ON THE TOPOGRAPHY-DRIVEN VORTICITY PRODUCTION IN SHALLOW LAKES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 03 May 2019, pp. 148-160
-
- Article
-
- You have access
- Export citation
Nonlinear systems coupled through multi-marginal transport problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 April 2019, pp. 450-469
-
- Article
- Export citation